STEOMETRIA
bluee: W ostrosłupie ABCS podstawa ABC jest trójkątem równoramiennym o ramionach AC i BC długości 4 i
kącie miedzy nimi 30. Punkt E− środek krawędzi AB − jest spodkiem wysokości tego ostrosłupa,
a krawędź boczna CS tworzy z podstawą kąt 60. Ostrosłup przecięto płaszczyzną przechodzącą
przez krawędź AB i mającą z przeciwległą krawędzią CS wspólny punkt D. Oblicz pole otrzymanego
przekroju wiedząc, że z podstawą ostrosłupa tworzy on kąt 75. Podaj dokładny wynik obliczeń.
8 lut 13:19
bluee:
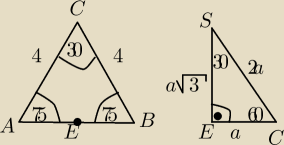
Czy dobrze sobie wyobrażam tą bryłę?
8 lut 13:28
bluee:
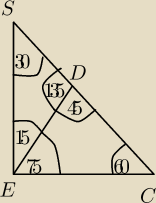
8 lut 13:31
bluee: .
8 lut 15:04
Basia:
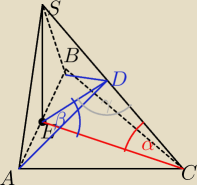
α=60
β=75
γ=45
△ADB jest równoramienny
z podstawy:
EC = 4*sin(75)
AE=4*sin(15)
AB = 2AE=8*sin(15)
z △CED i tw.sinusów
pozostaje podstawić wartości sin(45) i sin(60)
no i policzyć sin(15)
8 lut 15:27
Basia: albo lepiej policzyć AB z tw.cosinusów (tr.ABC)
8 lut 15:38
bluee: To zadanie z matury więc, a w karcie wzorów nie ma wartości funkcji trygonometrycznych kata 15
i 75. Więc tak korzystałam z tw. cosinusów, ale wychodzi pierwiastek stopnia.
8 lut 15:41
bluee: 4 stopnia
8 lut 15:42
Krzysiek60: sin(60o−45o) i masz sin15o
8 lut 15:43
bluee: Fakt. Dzięki za wskazówkę. Ale dlaczego nie wychodzi mi tw. cosinusów

8 lut 15:45
Basia:
z tw.cosinisów
| | √3 | | √3 | |
AB2 = 42+42−2*4*4*cos30 = 32−32* |
| = 32(1− |
| )= |
| | 2 | | 2 | |
AB = 4
√2−√3
z sinusa
| | √3 | | √2 | | 1 | | √2 | |
sin(15) = sin(60)*cos(45)−cos(60)*sin(45) = |
| * |
| − |
| * |
| = |
| | 2 | | 2 | | 2 | | 2 | |
AB = 2(
√6−
√2)
i to jest to samo, co widać po podniesieniu do kwadratu
(4
√2−√3))
2=16(2−
√3)
(2(
√6−
√2))
2 = 4(6−2
√12+2} = 4(8−4
√3)=16(2−
√3)
8 lut 16:00
bluee: DZIĘKI

8 lut 16:15
 Czy dobrze sobie wyobrażam tą bryłę?
Czy dobrze sobie wyobrażam tą bryłę?

 α=60
β=75
γ=45
△ADB jest równoramienny
z podstawy:
α=60
β=75
γ=45
△ADB jest równoramienny
z podstawy:

