Styczna do wykresu
Egz: Wyznacz styczną do wykresu funkcji f (x)= 1/x która jest równoległa do prostej y=−x
7 lut 22:59
Blee:
skoro ów styczna ma być równoległa do y=−x
to znaczy, że jest postaci y = −x + b
wzór na styczną w punkcie x
0:
y − f(x
0) = f'(x
0)(x − x
0) ⇔ y = f'(x
0)*x + ( f(x
0) − x
0*f'(x
0) )
tak, więc f'(x
0) =
−1
| | 1 | |
a wiemy, że f'(x) = − |
| czyli mamy dwa punkty w których może być ta styczna: x0 = −1 |
| | x2 | |
lub x
0 = 1
podstawiasz do wzoru na styczną w punkcie i masz równania dwóch prostych (stycznych) do f(x) i
będących równoległych do zadanej prostej.
7 lut 23:21
Basia:
a=−1
1 = x
2
x=1 ∨ x=−1
b=f(1) ∨ b=f(−1)
b=1 ∨ b=−1
mamy dwie styczne spełniające warunki zadania:
y=−x+1 y=−x−1
7 lut 23:23
Maciess: Jedna styczna wyszła mi y=−x+2 ale jeszcze będzie druga
7 lut 23:24
Maciess: Druga mi wyszła y=−x−2
Basiu, chyba masz błąd. Albo ja...

7 lut 23:28
Qulka:
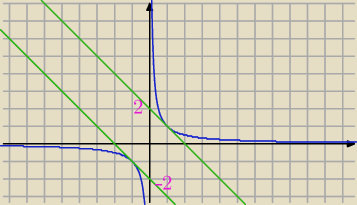
8 lut 00:54

