Geometria analityczna Partycja: Znajdź wzór stycznej do okręgu x²+y²+2x=0 przechodzącej przez punkt A=(1,1).

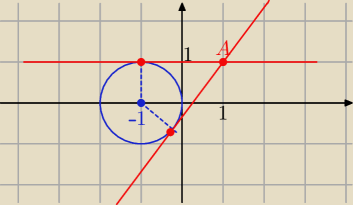
Krzysiek60: jak zrobisz rysunek to z tego co widze jedna styczna masz za darmo Teraz druga

Partycja: no właśnie z tą drugą mam problem

Eta: o: x²+y²+2x ⇔o: (x+1)²+y²=1 S(−1,0) , r=1 styczna ma równanie s: y=ax+b i A(1,1) ∊ s 1=a+b ⇒ b= 1−a więc styczna ma równanie y= ax+1−a w postaci ogólnej : ax−y+1−a=0 odległość środka S(−10) od stycznej jest równa r=1

	|−a+1−a|
i mamy:		=1 ⇒ |2a−1|=√a2+1 ^2 ( bo obydwie strony dodatnie
	√a2+1

otrzymując 4a²−4a+1=a²+1 ⇒ 3a²−4a=0 ⇒ a=0 lub a= 4/3 to b= 1 lub b= −1/3 zatem styczne mają równania s₁: y=1 s₂: y= (3/4)x−(1/3) ===========================

Eta: Oczywiście S(−1,0) ( przez nieuwagę wpisało mi S(−10)

Partycja: ok dzięki wielkie

Eta: