równoległobok mat: Dany jest równoległobok ABCD o kącie ostrym 30⁰ i bokach AB=15 i AD=8 Punkt M jest środkiem boku AD zaś punkt N znajduje sie na boku AB tak że AM: MB= 2:1 Odcinki MC i ND przecinają się w punkcie K Oblicz pole czworokąta ANKM rysunek zrobiony a dalej to klapa bardzo prosze o pomoc

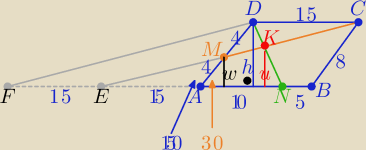
Eta: 1/rysunek zgodny z trescią zadania i na nim przedłużamy AB kreśląc równoległe proste DF i CE to |FN|=40 i |EN|=25 P(ANKM)= P(ΔENK)−P(ΔEAM) =======================

	1
P(ΔEAM)=		*15*4*sin150o = 15 , sin150o=sin30o=1/2
	2

wysokości w trójkątach "ekierkowych" o kątach 30^o, 60^o,90^o h=4 i w=2 Należy jeszcze wyznaczyć długość wysokości "u" z podobieństwa trójkątów EKN i FDN z cechy (kkk)

|FN|		h		40		4		5
	=		⇒		=		⇒ u=
|EN|		u		25		u		2

	1		5		125
zatem : P(ENK)=		*25*		=
	2		2		4

	125		65
to P(ANKM)=		−15 =		=16,25 [j2]
	4		4

==========================

Eta: Może ktoś ........ poda jeszcze inny sposób

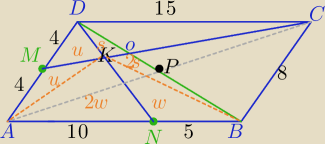
Mila: II sposób P_ABCD=60, P_ΔACD=30, P_AND=20, P_ΔNBD=10 1) MC i PD środkowe ΔACD stąd :

	1		30
|DO|=		|BD| i PΔMOD=		=5
	3		6

2) s,u,w− pola odpowiednich Δ jak na rysunku u+s=5 2u+2w=20⇔u+w=10 3s+w=10 −−−−−−−−−−−− w−s=5

	5
w+3s=10⇔s=
	4

	5
u=5−		=334
	4

−−−−−−−−−−−−−− P_ANKM=20−3³₄=16.25 ==================

Eta: A mat ma to i tak w d.........

Mila: Właśnie