czworokąt ABCD kwadrat: Czworokąt ABCD jest wpisany w okrąg. Punkty P i Q leżą odpowiednio na półprostych AB→ i AD→, przy czym AP = CD, AQ = BC. Wykazać, że środek odcinka PQ leży na prostej AC.

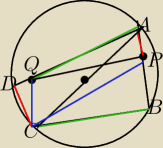
Pełcio: Podejrzewam, że czworokąt QCPA to równoległobok i byłoby po sprawie, ale chyba coś nie widzę, albo widzę źle

kwadrat: ja na razie wymyśliłem ze [APQ] = [BCD]

Mila: https://om.edu.pl/sites/default/files/zadania/om/67-2r_0.pdf