symetria takmatma: podaj równanie prostej symetrycznej do y= −3x − 3 względem prostej y = −x +1 jak zacząć proszę o wskazówki

Blee: Mozesz np w taki sposob: 1) wyznaczasz punkt przeciecia sie tych dwoch (znanych ci) prostych. Wyznaczana prosta takze musi sie przecinac w tym punkcie. 2) wybierasz sobie jakis punkt na prostej y=−x+1 i prowadzisz prosotpadla do tej prostej przechodzaca przez ten punkt (punkt inny niz w pkt 1). 3) wyznaczasz punkt przeciecia sie tej prostopadlej z prosta y=−3x − 3. 4) wyznaczasz dlugosc odcinka pomoedzy tymi dwoma punktami i wyznaczasz punkt na tej prostopadlej bedacy odlegly o taka sama odleglosc. 5) masz dwa punkty (z 1 i 4) ... prowadzisz prosta przez te dwa punkty Czy jest to najszybszy sposob, nie wiem. Czy ten sposob wymaga jakis skomplikowanych wzorow, nie.

takmatma: Dziękuję. myślałam, że jest krótszy sposób

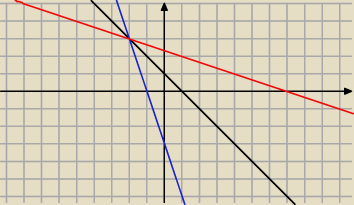
PW: Na ilustracji czarna prosta y=−x+1, niebieska y=−3x−3, czerwona szukana prosta

	1		7
y=−		x+		.
	3		3

Trzeba wymyślić wzór na symetrie względem prostej y=−x+1. Jest to dość łatwe, bo symetria względem prostej y=−x działa tak, że punktowi (x₀, y₀) przyporządkowuje punkt (−y₀,−x₀). Chcąc przekształcić P=(a,b) za pomocą symetrii o osi y=−x+1 przesuwamy punkt i oś o wektor [0,−1]. Otrzymujemy punkt Q=(a,b−1) i prostą y=−x. Obraz Q w symetrii o osi y=−x jest punktem Q'=(−b+1,−a). Po przesunięciu "z powrotem" o wektor [0,1] otrzymamy punkt P'=(−b+1,−a+1), który jest obrazem P w symetrii o osi y=−x+1. Podsumowanie: (a,b) → (−b+1,−a+1) jest "wzorem na symetrię" względem prostej y=−x+1. Jeżeli przekształcamy punkt P należący do prostej y = −3x−3, czyli punkt o pierwszej współrzędnej x, a drugiej −3x−3, to (x,−3x−3) → (−(−3x−3)+1, −x+1), a więc punkty leżące na szukanym obrazie prostej mają współrzędne x'=3x+4, y'=−x+1. Aby pokazać związek między x' a y' , czyli równanie prostej, mnożymy drugie równanie przez 3 i dodajemy stronami: x'+3y'=7

	1		7
y'=−		x'+		.
	3		3

Te "primy" były tylko dla odróżnienia współrzędnych prostej i jej obrazu, równanie szukanej prostej ma postać

	1		7
y=−		x+		.
	3		3

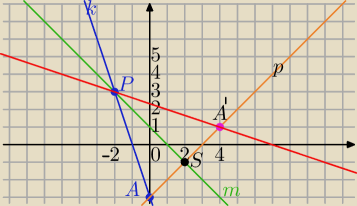
Mila: k: y=−3x−3 m: y=−x+1 1) Punkt przecięcia : −x+1=−3x−3⇔x=−2 i y=3 P=(−2,3) obrazem punktu P w symetrii względem prostej m jest ten sam punkt P'=(−2,3) 2) A=(0,−3) ∊k Prostopadła do m przechodząca przez punkt A p: y=x−3 4) punkt przecięcia prostych m i p x−3=−x+1⇔x=2 i y=−1 ⇔S=(2,−1) 5) S jest środkiem odcinka AA', gdzie A' jest symetryczny do A wzgledem prostej m A'(a,b):

	0+a		−3+b
2=		i −1=		⇔a=4 i b=1
	2		2

A'=(4,1) 6) prosta A'P y=ax+b i A',P∊do prostej 1=4a+b i 3=−2a+b

	1		7
a=−		i b =
	3		3

	1		7
n: y=−		x+		wzór szukanej prostej
	3		3

===================================

takmatma: Bardzo dziękuję