Rozkład prawdopodobieństwa Reqqu: Witam, nie za bardzo wiem jak zacząć to zadanie, nie rozumiem co właściwie trzeba wyliczyć. Znajdź przekształcenie, które z liczb o jednorodnym rozkładzie prawdopodobieństwa na przedziale

	C
(0,1) pozwoli uzyskać liczby o gęstości prawdopodobieństwa f(x)=
	u   √   d

dla x ∊ (d,9d). Znany parametr 'd' jest dodatni, stałą C należy wyznaczyć samodzielnie.

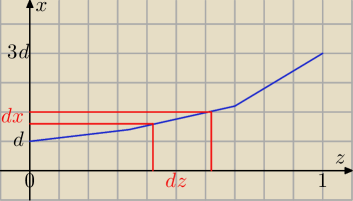
g: Zmienna losowa Z ma rozkład jednostajny na odcinku (0,1). Szukamy funkcji x = g(z) takiej że funkcja gęstości pr. f(x) jest określona. Na rysunku niebieska linia symbolizuje g(z). Musi być spełnione dz = f(x)*dx, i jednocześnie mamy dx = g'(z)*dz. Stąd

	1
g'(z) =
	f(g(z))

Ja bym to rozwiązywał numerycznie, np. tak: dz = 0,001 z₀ = 0 g(z₀) = d z_k+1 = z_k + dz

	dz
g(zk+1) = g(zk) +
	f(g(zk))

Iteracja kończy się na z_k = 1 i wtedy g(1) powinno wyjść 3d.

g: 9d, nie 3d.