pomocy
marta: Dane są funkcje y= − ½ x – 2 i y= − x + 1
a) Sporządź wykresy tych funkcji w jednym układzie współrzędnych.
b) Oblicz miejsca zerowe tych funkcji.
c) Oblicz pole figury ograniczonej tymi wykresami oraz osiami układu współrzędnych.
6 lut 11:04
Marta: Jak to zrobić?
6 lut 14:22
Marta: ?
6 lut 14:47
chmielu037: narysuj układ współrzędnych narysój dwie proste tam gdzie przetną sie z osią OX to będa
miejsca zerowe
6 lut 14:54
Marta: narysowałam dwie proste przecieły sie ale nie wyszła mi żadna figura ; (
6 lut 14:59
chmielu037: no musi napewno jakiś wielokąt wyjsc pamietaj ze i osie układu współrzednych też ograniczają
ten wielokąt i napewno bedzie go można podzielić na jakies 2 proste trójkąty np których pole
łatwo można obliczyć a potem zsumowac

6 lut 15:02
Godzio: pomoge
6 lut 15:54
Godzio:
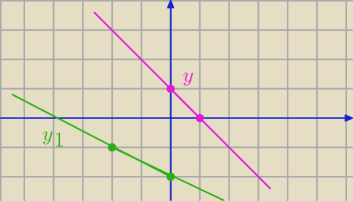
x 0 −2
−−−−−−−−−−−−
y −2 −1
y=−x+1
x 0 1
−−−−−−−
y 1 0
wykres troche za mały ale się tam gdzieś na dole przetną a punkt w którym się przetną
obliczymy:
y
1=y
−x −4 = −2x +2
x = 6
x=6 y = −5
A(6,−5)
i powstał nam trójkąt o podstawie na osi X
h = |OA| = 5
Miejsca zerowe:
0 = −x −4
x =−4
B(−4,0)
y = −x +1
0 = −x +1
x = 1
C(1,0)
podstawa tójkąta: a
a=|BC| = 5
| | ah | |
P = |
| = U{25}{2] = 12,5
|
| | 2 | |
6 lut 16:04
7 lut 12:36
Marta: Tylko coś chyba wyszło nie tak bo z tyłu w książce pisze że powinno wyjść 8,5 pole
skąd wiesz ze Bc ma 5?
7 lut 12:44
Marta: 
7 lut 12:57
Marta: ? ? ? ?
7 lut 13:01
Marta: ? ? ? ? ? ? ? ? ? ? ?
7 lut 13:28
Marta: 

7 lut 13:43
Marta: 
7 lut 14:29
Marta: jak to obliczyć tą figurę?
7 lut 14:37
Marta: 
?
7 lut 14:43
Bogdan:
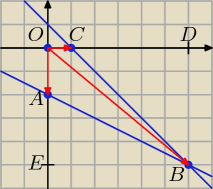
Obliczamy współrzędne wierzchołków czworokąta: OABC rozwiązując odpowiednie równania.
O = (0, 0), A = (0, −2,), B = (6, −5), C = (1, 0)
→
OA = [0, −2],
→
OB = [6, −5]
→
OC = [1, 0]
Obliczmy wartości wyznaczników:
| 0 −2 |
W
OAB = | | = 12
| 6 −5 |
| 6 −5 |
W
OBC = | | = 5
| 1 0 |
| | 1 | | 1 | |
Pole P{OABC} = |
| *|12| + |
| *|5| = 6 + 2,5 = 8,5 [j2] |
| | 2 | | 2 | |
Innym sposobem na obliczenie wartości pola czworokąta jest:
P
OABC = P
OEBD − (P
ΔAEB + P
ΔCBD)
7 lut 15:17









 ?
?
 Obliczamy współrzędne wierzchołków czworokąta: OABC rozwiązując odpowiednie równania.
O = (0, 0), A = (0, −2,), B = (6, −5), C = (1, 0)
→
OA = [0, −2],
→
OB = [6, −5]
→
OC = [1, 0]
Obliczmy wartości wyznaczników:
| 0 −2 |
WOAB = | | = 12
| 6 −5 |
| 6 −5 |
WOBC = | | = 5
| 1 0 |
Obliczamy współrzędne wierzchołków czworokąta: OABC rozwiązując odpowiednie równania.
O = (0, 0), A = (0, −2,), B = (6, −5), C = (1, 0)
→
OA = [0, −2],
→
OB = [6, −5]
→
OC = [1, 0]
Obliczmy wartości wyznaczników:
| 0 −2 |
WOAB = | | = 12
| 6 −5 |
| 6 −5 |
WOBC = | | = 5
| 1 0 |