Całki pierwiastka Przemek: kurcze dostalłęm cos takiego na pd i nie wiem jak to ruszyc ∫√1−x²

Blee: Na 'pd' ? Pelnymi slowami pisac nie umiemy? O dx nie pamietamy? Student ... ojjj student. A calke zrobisz przez czesci.

bezendu:

	1		1
∫√1−x2dx=		(arcsin(x)+		(2arcsin(x)))+C
	2		2

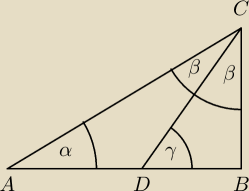Mariusz: Od amerykańców wziąłbym jedynie pomysł na trójkąt prostokątny przypominający podstawienia dla całek postaci ∫R(x,√ax²+bx+c)dx oraz ∫R(sin(x),cos(x))dx W trójkącie ABC mamy dane długości dwóch boków których stosunek daje sin(α),tan(α),sec(α) (w twoim przypadku sin(α)) Obliczasz tan(γ) np korzystając z twierdzenia Pitagorasa i z twierdzenia sinusów tan(γ) da ci podstawienie dla całek postaci ∫R(x,√ax²+bx+c)dx Jeśli odwrócimy trochę to zadanie tzn tan(γ) uznamy za dane a sin(α) oraz cos(α) za szukane to pokażemy że podstawienie tan(γ) sprowadzi całkę postaci ∫R(sin(x),cos(x))dx do całki z funkcji wymiernej Przez części będzie jednak najwygodniej

	−x2
∫(x)'√1−x2dx=x√1−x2−∫		dx
	√1−x2

	1−x2−1
∫√1−x2dx=x√1−x2−∫		dx
	√1−x2

	1
∫√1−x2dx=x√1−x2−∫√1−x2dx+∫		dx
	√1−x2

2∫√1−x²dx=x√1−x²+arcsin(x)+C₁

	1
∫√1−x2dx=		(x√1−x2+arcsin(x))+C
	2