trójkąt, dwusieczna Ania: W trójkącie o bokach długości 3 ; 3,5 ; 4,4 na najdłuższym boku znajduje się punkt równooddalony od dwóch pozostałych boków. Wyznacz długość odcinków na jakie dzieli ten punkt najdłuższy bok trójkąta. W odpowiedziach ten szukany punkt należy do dwusiecznej kąta(kąta, który znajduje się naprzeciw najdłuższego boku). Mógłby mi ktoś dokładnie wytłumaczyć dlaczego?

Basia: P∊dwusiecznej kąta ⇔ jest równo oddalony od ramion kąta

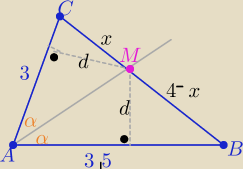
Eta: Dwusieczna kąta jest zbiorem punktów równo oddalonych od ramion kąta To w tym zadaniu spełniony jest ten warunek czyli ten punkt leżący na najdłuższym boku leży jednocześnie na dwusiecznej kąta między bokami o długościach 3 i 3,5 Teraz skorzystaj z własności dwusiecznej

3		3,5
	=		⇒ x=|CM|= ........... to |BM|= 4−x=............
x		4−x

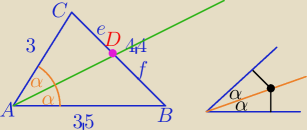Mila: Dwusieczna kąta jest zbiorem punktów jednakowo odległych od ramion kąta . Z twierdzenia o dwusiecznej kąta wewnętrznego trójkąta mamy:

|AB|		|AC|
	=		i e+f=BC⇔
f		e

3.5		3
	=		⇔3f=3.5e
f		e

f=4.4−e 3*(4.4−e)=3.5e 13.2−3e=3,5e 6.5e=13.2

	13.2
e=		≈2.03
	6.5

f=4.4−2.03 albo licz dokładną wartość

Eta: Oj sorry zamiast 4,4 napisałam 4 poprawiam: 3(4,4−x)=3,5*x ⇒ 13,2−3x=3,5x ⇒ 6,5x=13,2 ⇒ x=|MC|= 132/65

	22		132		22*13−132
to |BM|=		−		=		=154/65
	5		65		65

Odp: |MC|=132/65 , |BM|=154/65 =========================== co daje w sumie : (132/65)+(154/65)= 256/65 = 4,4 czyli ok