Stereometria UczącySię: Witam, mam takie zadanie: Na przekątnych AB i CD sąsiednich ścian bocznych sześcianu (przekątne AB i CD leżą na prostych skośnych) wybrano punkty E i F tak, że:

AE		DF
	=		= 2
EB		FC

Wykaż, że odcinek EF jest prostopadły do przekątnych AB i CD. Jakieś wskazówki ? Szczerze to nie do końca znam własności tych prostych skośnych

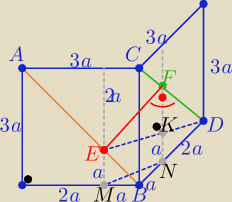Eta: AB i DC −−−skośne przekątne sąsiednich ścian 3a−−długość boku sześcianu to |AB|=|CD|= 3a√2 Z treści zadania : |AE|=|DF|=2a√2 i |BE|=|CF|=a√2 i |∡ABD|=90^o ( trzy proste prostopadłe) rzuty prostokątne punktów E i F na krawędzie podstawy dzielą krawędź 3a też w stosunku 2:1 zatem |MB|=|BN|=a i w trójkącie prostokątnym EBD z tw. Pitagorasa |ED|² =2a²+9a²= 11a² ================== |FN|=2a i |EM|=|KN|=a ΔKEF jest też prostokątny |EK|=|MN|= √a²+a²=a√2 i |FK|=a z tw. Pitagorasa |EF|²=3a² Mamy wykazać ,że EF ⊥CD Sprawdzamy czy trójkąt AFD jest prostokątny ( odwrotne tw. Pitagorasa |EF|²+|FD|² =3a²+(2a√2)² =3a²+8a²=11a²=|ED|² ========== Zatem EF ⊥CD i do AB co kończy dowód P.S. Bardzo ładne i ciekawe zadanko Mam nadzieję,że wszystko teraz już rozumiesz No to ......... pora do

UczącySię: Zadanko ciekawe, bo jestem w 3liceum i mamy taki kurs który prowadzi pani z uczelni i ona ma takie. Dla mnie większość jest bardzo trudna niestety

UczącySię: I dziękuję bardzo za rozwiązanie, rozumiem