geometria trójkąta i okręgów Piotrek: W trójkącie ABC: kątB = 120°, |AC| = 7, |AB| = 3. Uzasadnij, że stosunek długości promienia okręgu opisanego na tym trójkącie do długości promienia okręgu wpisanego w ten trójkąt jest mniejszy niż 5.

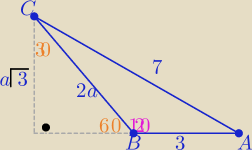
Eta: 1/ rysunek

	7		7√3
2/ z tw. sinusów R=		⇒ R=
	sin120o		3

3/ z tw. cosinusów 7²= 4a²+9+2*2a*3*(1/2) bo cos120^o= −1/2 i a >0 to 4a²+6a−40=0 ⇒ .... a=5/2

	1		15√3
to |BC|=2a= 5 i P(ABC)=		*3*a√3 = ...........=
	2		4

4/ P=r*p , p−−− połowa obwodu

	2P		√3
to r=		⇒ .......... r=
	3+7+5		2

	R		14
to		= ......... =		<5
	r		3

c.n.u.

Marcin: R nie powinno być 14√3/3?

janek191:

	√3
R JEST ŹLE OBLICZONE, BO SIN 120o =
	2

Eta: Jest ok bo R=7√3/3 i r=√3/2

	7√3		2
to R/r=		*		= 14/3
	3		√3

Eta: Raaaaaaaaaaaacja R= 14√3/3

Marcin: No i teraz nie wychodzi

Eta: Wszystko dobrze napisałam ! Janek mi namieszał !

	7		7√3
z tw sinusów 2R=		⇒ R=		( jest ok
	sin120o		3

Marcin: Dziękujemy Eta <3

Eta: Na zdrowie