Ktoś chce pomóc? Tomandero: Oblicz długość promienia okręgu wpisanego w trójkąt prostokątny, jeśli wiemy , że długość boków tego trójkąta twarzą ciąg arytmetyczny o roznicy 3.

Satan: a² + (a + 3)² = (a + 6)² a² + a² + 6a + 9 = a² + 12a +36 a² − 6a − 27 = 0 Rozwiązujesz, założenia uwzględniasz, wyliczasz promień ze wzorku.

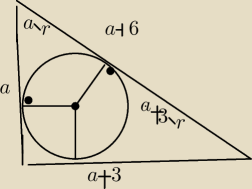
Krzysiek60: a+6= (a−r)+[(a+3)−r] a²+(a+3)²= (a+6)² a>0 i r>0

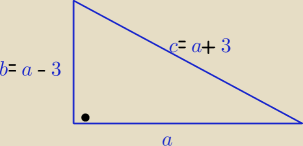
Eta: 1/ Boki takiego trójkąta : a, b= a−3, c= a+3 , a>3 z tw. Pitagorasa a²+(a−3)²= (a+3)²⇒ ............ ⇒ a=12 to a=12, b=9, c=15

	a+b−c
rw=		=............
	2

Tomandero: A wyjaśnisz jeszcze dlaczego r=a+b−c/2 ? I dlaczego b= a −3 ?

Tomandero: A dobra na ten promień to jest taki wzór

Eta:

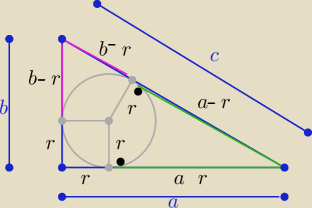
	a+b−c
c=a−r+b−r ⇒ 3r=a+b−c ⇒ rw=
	2

masz ten wzór w tablicach wzorów maturalnych Długości boków tworzą ciąg arytmetyczny o różnicy r=3 to mogę je zapisać jak wyżej Koledzy wpisali a, a+3, a+6 lub tak a−3, a, a+3

Satan: Eta boki obrała tak, by było jak najłatwiej policzyć deltę − przynajmniej tak myślę. Co do wzoru, to wyprowadzenie jest właściwie wszędzie

Tomandero: Dziękuję ci bardzo normlanie lepiej wytłumaczone niż na lekcji

Tomandero: Noo twraz widzę i rozumiem to dziękuję wam bardzo za pomoc jutro sprawdzinik i wolałem się dopytać