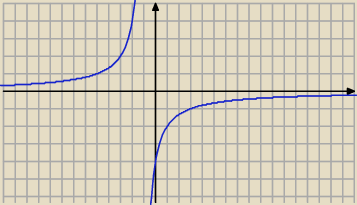
nierownosci wymierne bartek: cześć, mam takie zadanie: ^2x−2_x+1>2 ,x≠−1 ^2x−2_x+1−2>0 ^{2x−2−2x−2}_x+1>0 x=−1 (tu powinien być wykres, ale nie wiem jak zrobić) i wyszło mi, że x∊(−∞;−1) dobrze robię? z góry dzięki B)

Eta: x≠−1

2x−2−2(x+1)
	>0
x+1

−4
	>0 ⇔ x+1<0 ⇒ x<−1
x+1

x∊(−∞, −1)

bartek: a kiedy mnożę całe obustronnie przez "−1" zeby zmienić znak nierówności? wiem, że tak się robi, ale nie wiem kiedy... wytłumaczysz?

Eta:

−4
	>0 −4<0 to x+1<0
x+1

Krzysiek60:

2x−2
	>2 dla x≠−1
x+1

2x−2
	−2>0
x+1

2x−2−2(x+1)
	>0
x+1

−4
	>0
x+1

	−4
wykres		(niebieski
	x+1

mnozymy przez kwadrat mianownika −4(x+1)>0 −4x−4>0 −4x>4 x<−1 (dobrze masz ale na drugi raz przedstaw swoje obliczenia

bartek: ej a co z tym "mnożeniem przez minus jeden" i z tą "zmianą znaku"?

Eta: Po co "kwadrat" mianownika ? Ułamek o liczniku ujemnym ma wartość dodatnią wtedy gdy mianownik jest ujemny! i po ptokach zatem x+1<0

UczącySię:

	−4
Wiesz po prostu, że −4 jest ujemne, więc jesli		>0 to automatycznie mianownik musi być
	x+1

mniejszy bo wtedy te minusy się skrócą

Maciess: To co piszecie to logicze, ale metoda z kwadratem mianownika jest łatwa do zapamiętania i zwalnia z myślenia

Eta:

	x−2
(		<0 , x≠1
	x−1

zamiana na równoważną postać iloczynową (x−2)(x−1)<0 ⇒ x∊(1,2) i też "zwalnia od myślenia" ... choć w matematyce to poprawne myślenie jest połową sukcesu!