Geometria dowód julia.lewandowska: W czworokącie połączono kolejno środki boków. Wykaż, że powstały w ten sposób równoległobok ma pole dwa razy mniejsze od pola danego czworokąta

PW: Czworokąt podziel na dwa trójkąty za pomocą odcinka łączącego dwa "przeciwległe" wierzchołki. W każdym z tych trójkątów mamy opisany w zadaniu odcinek łączący środki boków. Jak wiadomo odcinek ten jest równoległy do podstawy i jego długość jest połową długości podstawy. W ten sposób mamy dwa "duże trójkąty" o sumie pól równej polu czworokąta i dwa "małe". Mały

	1
jest podobny do dużego, stosunek długości boków jest równy		, a więc stosunek pól jest
	2

	1		1
równy		− dwa małe trójkąty mają sumę pól równą		pola czworokąta.. Połączenie
	4		4

dwóch innych "niekolejnych" wierzchołków i przeprowadzenie takiego samego rozumowania pozwala

	1		1
stwierdzić, że małe trójkąty mają sumę pól równą 2.		=		pola czworokąta.
	4		2

\"Lepiej matematycznie" wyrazisz to na podstawie rysunku z oznaczonymi wierzchołkami czworokąta i środkami boków.

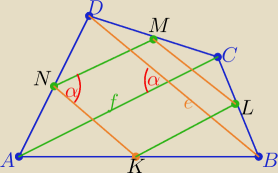
Eta: To jeszcze taki sposób e, f−−− dł. przekątnych czworokąta i α −− kąt między nimi

	1
to P(ABCD)=		f*e*sinα
	2

Czworokąt KLMN jest równoległobokiem jego boki mają długość

1		1
	e i		f i kąt między tymi bokami też jest α
2		2

( bo boki są równoległe do przekątnych czworokąta ABCD

	1		1		1
zatem P(KLMN) =		f*		e*sinα=		e*f*sinα
	2		2		4

	1
zatem P(KLMN)=		P(ABCD)
	2

c.n.w