Rownania wszystkich wspolnych stycznych Hejeczka: Wyznacz równiania wszystkich wspólnych stycznych do paraboli o równaniu y=¹₂x² i okręgu o równaniu x²+(y+⁵₂)²=2

Hejeczka: Siedze nad tym pare godzin i ciagle mi nie wychodzi. Bardzo prosze o pomoc

Mila: To napisz odpowiedź, przeliczę.

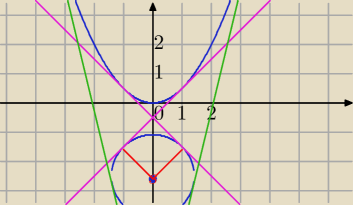
Hejeczka: Są 4 styczne: y=x−¹₂ y=−x−¹₂ y=√17x−¹⁷₂ y=−√17x−¹⁷₂

Mila:

	1
f(x)=		x2
	2

1) Styczna do paraboli:

	1
(a,		a2)− punkt styczności z parabolą
	2

	1
s: y=f'(a)*(x−a)+		a2
	2

	1
2) f'(x)=		*2x=x
	2

f'(a)=a

	1
s: y=a*(x−a)+		a2
	2

	1		1
s: y=ax−		a2 ⇔ax−y−		a2=0
	2		2

	5
3) S=(0,−		) − wsp. środka okręgu , r=√2
	2

Odległość stycznej od środka okręgu jest równa r=√2

	5   1   |a*0−(− )− a2|   2   2
d(s,S)=		=√2⇔
	√a2+1

	5		1
|		−		a2|=√2*√a2+1
	2		2

|5−a²|=2√2√a²+1 /² 25−10a²+a⁴=8(a²+1) 25−10a²+a⁴−8a²−8=0 a⁴−18a²+17=0 Δ=256

	18−16		18+16
a2=		=1 lub a2=		=17
	2		2

a=1 lub a=−1 lub a=√17 lub a=−√17 Styczne:

	1
s1: y=x−
	2

	1
s2: y=−x+
	2

	17
s3: y=√17x−
	2

	17
s4: y=−√17x−
	2

Mila: s₂ źle napisałam, ale dobrze narysowałam.

	1
s2: y=−x−
	2

jc: Styczna do paraboli w punkcie (p,p²/2): px−y−p²/2=0. Która styczna leży w odległości √2 od środka okręgu czyli od punktu (0,−5/2)? U{|5/2 − a²/2|}{√a²+1=√2 2(a²+1)=(5/2−a²/2)² a⁴−10a²+25=8a²+8 a⁴−18a²+17 = 0 a=±1, a=±√17 ...

jc: Oj, po drodze zmieniłem p na a, a właściwie było odwrotnie, najpierw a, a potem przez moment p. Mila, liczyć deltę jak widać jeden z pierwiastków? Zawsze odradzam rachunków, jak widać wynik. W rachunkach można się przecież pomylić.

Hejeczka: Mila mogłabyś wytłumaczyć z kąd wzięłaś d(s, S)

Mila: "skąd" Odległość punktu P(x₀,y₀) od prostej ( równanie w postaci ogólnej): k: Ax+BY+C=0

	|A*x0+B*y0+C|
d(P,k) =
	√A2+B2

W Twoim zadaniu : ( przed 3 punktem)

	1
s: ax−y−		a2} =0 styczna do paraboli, ma być wspólną styczną z okręgiem.
	2

Hejeczka: Dobra to już wszystko rozumiem. Dzięki wielkie

Mila: