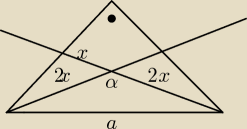
W trójkącie Bell: Pomocy w trójkącie prostokątnym równoramiennym poprowadzono srodkowe kątów ostrych oblicz cosinus kąta rozwartego zawartego miedzy nimi.

Godzio:

	1
(		a)2 + a2 = (3x)2
	2

a² + 4a² = 36x²

5a2
	= x2
36

	a√5
x=
	6

	a√5
2x =
	3

i z tw cos a² = (2x)² + (2x)² − 8x² * cosα

	10a2		5a2
a2 =		− 8 *		* cosα
	9		36

9a2−10a2		10a2
	= −		cosα
9		9

−a² = −10a²cosα

	1
cosα =
	10

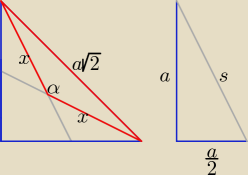Bogdan: Kąt α jest kątem rozwartym, cosα < 0.

	1		2		2		1		1
s = √ a2 + a2/4 =		a√5, x =		s =		*		a√5 =		√5
	2		3		3		2		a

Z twierdzenia cosinusów: 2a² = x² + x² − 2x²cosα

	5		5		9		4
2*		a2cosα = 2*		a2 − 2a2 / *		⇒ cosα = −
	9		9		10a2		5

Godzio: ano tak a√2 a nie "a"