wzór na srodkową trójkata Trójkąt: Podstawa AB trójkąta równoramiennego ABC ma długość 8 oraz |∡BAC | = 30 stopni. Oblicz długość środkowej AD tego trójkąta. moje rozumowanie: |∡ACB | = 120 stopni x = AC = BC policzyłam x z tw. cosinusow, wyszło x=⁸_√3 (na plusie, nie wiem czemu wyswietla się na minusie) wiem, ze dalej mogę z tw. cosinusów, ale chciałam wykorzystać wzór na srodkową trójkąta: https://pl.wikipedia.org/wiki/%C5%9Arodkowa_tr%C3%B3jk%C4%85ta AD = ¹₂ √ ⁶⁴₃*2 +64*2 − ⁶⁴₃ = ¹₂ √ ⁴⁴⁸₃ a powinno wyjść ^4√21₃ wiem, że to głupie może, ale nie mogę znaleźć błędu (x jest dobrze wyliczone) z góry dziękuję

Trójkąt: pomocy

Trójkąt: juz wiem

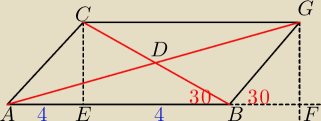
Hajtowy: D − punkt przecięcia przekątnych Trochę nie do końca widać, że |AE| = |BF| = 4 ale myślę, że rozumiesz

GF		4√3
	= tg30o ⇒ GF =
BF		3

	1		1		1		1
AD =		AG =		√AF2+GF2 =		√144+489 =		*4*√9+39 = ...
	2		2		2		2

	4√21
... = 2√849 =		= |AD|
	3

Hajtowy: Już wiesz a ja się napracowałem

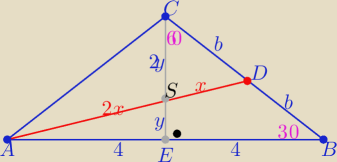Eta: Środkowe dzielą się w stosunku 2:1 licząc od wierzchołka W ΔEBC "ekierce" o kątach 30^o,60^o,90^o

	4√3
|EB|=3y√3 =4 ⇒ y=
	9

z tw. Pitagorasa w ΔAES

	16		4
4x2= 16+		/ :4 ⇒ x2=4+		⇒ x2=112/27
	27		27

	4√7		4√21
x=		=
	3√3		9

	4√21
to |AD|=3x=
	3

==================

Hajtowy: Pięknie Eta

Eta:

Eta: Można dokończyć też tak: x²=112/27 to 9x²= 112/3⇒ 3x=|AD|=4√21/3