Graniastoslup prawidlowy trojkatny - zadanie 4 astrolog: Graniastoslup prawidlowy trojkatny o krawedzi podstawy a przecieto plaszczyzna przechodzaca przez krawedz dolnej podstawy i srodki dwoch krawedzi gornej podstawy. Otrzymany przekroj ma pole rowne a² Oblicz cosinus kata jaki plaszczyzna przekroju tworzy z dolna podstawa graniastoslupa

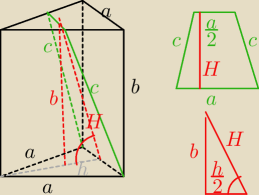
sylwia: Przekrój jest trapezem o podstawach a i ^a₂ ponieważ podstawy są trójkątami równobocznymi, a "górny" został "przekrojony" w połowach boków. Jego pole wynoszące a² można opisać wzorem ¹₂(a+^a₂)*H=a² stąd H=⁴₃a Wysokość podstawy czyli trójkąta równobocznego wynoszącą ¹₂(a√3) wysokość b dzieli na połowy a zatem z trójkąta prostokątnego (czerwonego) cos zaznaczonego kąta nachylenia płaszczyzny przekroju do podstawy wynosi: ^h₂ : H = ¹₄(a√3)*³_4a=^3{√3₁₆