nie śpimy
Patłyk2703: parę rzeczy do sprawdzenia:
1,Tworzymy uporządkowane pary z liter słowa OJCZYZNA.
a) Ile jest par złożonych z różnych liter?
b) Ile jest par, w których pierwsza litera jest samogłoską, a druga spółgłoską?
A jeśli użyjemy liter słowa RZECZPOSPOLITA?
a)7*6*2
b)3*4
dla Rzeczpospolita
a)11*10*2
b)7*4
2.Ile różnych wyników można otrzymać sumując co najmniej dwie spośród liczb: 1,3,5,10,20,50,82?
wg mnie:
27−8−4
27 (liczba podzbiorów)
8− liczba podzbiorów 1 elementowych i ∅
4− liczba powtórzonych wyników, a dokładniej:
83=20+10+50+3=82+1
88=82+5+1=80+5+3
85=80+5=82+3
86=80+6=82+1+3
80=10+20+50
4 lut 00:01
Patłyk2703: 3. Oblicz, na ile sposobów można wybrać z talii 52 kart po jednej karcie z każdego koloru oraz
ile
jest takich wyborów, jeśli wśród wyjętych kart nie może być ani jednej pary kart o tej samej
wartości.
po jednej z tego samego koloru: 134
druga część zadania: 13*12*11*10*4!
4 lut 00:10
Patłyk2703: 4. W trzydziestoosobowej klasie dwudziestu uczniów uczy się łaciny, czternastu greki, a
dziesięciu
hebrajskiego. Jeśli żadne dziecko nie uczy się wszystkich trzech języków, a ośmioro nie uczy
się żadnego, to ilu uczy się greki i hebrajskiego?
wiemy, że
x=30
ł=20
g=14
h=10
ł∩g∩h=0
ł∪g∪h=22
ł+g+h−ł∩g−g∩h−ł∩h=22
20+14+10−ł∩g−g∩h−ł∩h=22
22=ł∩g+g∩h+ł∩h
po metodzie prób i błędów (niestety nic lepszego nie wymyśliłem)
ł∩g=12
g∩h=8
ł∩h=2
greki i hebrajskiego uczy się 8.
przy okazji, wiecie jak to zrobić bez metody prób i błędów?
4 lut 00:54
Patłyk2703: rzuci ktoś okiem? To samo sprawdzenie

4 lut 16:59
iteRacj@: u Ciebie
ł∩g=12
g∩h=8
z warunków zadania żadne dziecko nie uczy się wszystkich trzech języków i czternaścioro uczy
sie greki
czyli u Ciebie greki co najmniej 20 osób, to daje sprzeczność
4 lut 17:32
Patłyk2703: sorry, odwrotnie, g∩h=2, ł∩h=8
wtedy mamy g=14, bo 12+2
h=10 bo 8+2
ił=20 bo 12+8
4 lut 18:00
Pytający:
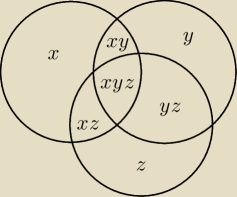
1.
a) 7*6, 11*10
b) ✓
2.
✓
3.
13
4 ✓
| | | |
13*12*11*10, ewentualnie | 4! |
| | |
4.
Oznaczenia jak na rysunku (to żadne mnożenia):
x+xy+xz+xyz=20 // łacina
y+xy+yz+xyz=14 // greka
z+xz+yz+xyz=10 // hebrajski
xyz=0
x+y+z+xy+xz+yz+xyz=22
2*22=2*(x+y+z+xy+xz+yz)=20+14+10=x+xy+xz+y+xy+yz+z+xz+yz ⇒
⇒ x+y+z=0 ⇒ x=y=z=0
Zatem:
xy+xz=20
xy+yz=14
xz+yz=10
⇒
xy=12 // łacina i greka
xz=8 // łacina i hebrajski
yz=2 // greka i hebrajski
4 lut 18:40
Patłyk2703: a jak z zadaniem 1,2, i 3cim? Z tego wątku.
4 lut 22:33
Pytający:
O cóż pytasz?

4 lut 22:55
Patłyk2703: o poprawność podanych tam przeze mnie odpowiedzi

4 lut 23:31
Pytający:
Przejrzyj jeszcze raz ten wątek.

5 lut 00:11
Patłyk2703: przepraszam, to przez burzę mózgów przed jutrzejszym egzaminem. Dziękuję Pingwinku

5 lut 00:23
Patłyk2703: Zdane na 4. Dzięki Dla Pytającego, Mili, i kilku innych którzy pomagali w tamtą piękną noc w
zadaniach

6 lut 16:03

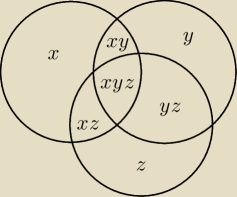 1.
a) 7*6, 11*10
b) ✓
2.
✓
3.
134 ✓
1.
a) 7*6, 11*10
b) ✓
2.
✓
3.
134 ✓




