szachownica :* Patłyk2703: Proszę o sprawdzenie: Na ile sposobów można ustawić dwa króle na szachownicy o wymiarach n × m tak, aby nie stały na sąsiadujących polach? wg mnie: 4*(1*(64−4)) narożniki 4*(6*(64−6)) wszystkie pola ze współrzędnymi: a,h,1,8, 36*(1*(64−9)) pozostałe pola, czyli kwadrat 6x6 od b do g i od 2 do 7 czyli razem mamy 4*60+4*6*58+36*55=3612

Mila: Też mam taki wynik, ale nie jestem mocna w szachach

Patłyk2703: też jestem średni, jak będziesz we Wro to możemy sobie coś pograć

Mila: To jest dobry wynik. Byłam we Wrocławiu na kursie i zawzięcie całymi wieczorami grałyśmy z koleżanką w szachy. W końcu udało mi się pokonać ją kilka razy pod rząd więc wywróciła szachownicę i wracałyśmy osobno do Krakowa. Po powrocie do biura już była zgoda

Mila: Mam drugi sposób. Ale, jeszcze go przemyślę.

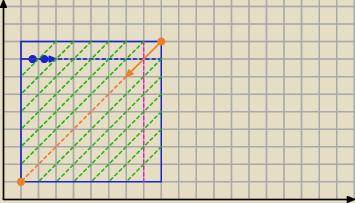
Mila: II sposób

64 2
	*2!=64*63 =4032

1)obok siebie w poziomie − 7*8*2!=112 2) obok siebie w pionie − 7*8*2!=112 3)obok siebie na ukos: pod linią pomarańczową 21*2=42 i nad nad linią 42 drugi ukos 2*42=84 przekątne główne; 2*7+2*7=28 84+84+28=196 ========== 4032−(2*112+196)=3612

Mila: Dobranoc

Patłyk2703: Dobranoc, będę w Krakowie to dam znać

Patłyk2703: i w sumie dziękuję, bo pod tym postem nie podziękowałem.

Mila: Na ten ukos wymyśl wzór, bo trochę liczyłam na piechotę.

Pytający: Ogólnie można tak zapisać: mn(mn−1)−2(m(n−1)+n(m−1)+(m−1)(n−1)+(m−1)(n−1))= =mn(mn−1)−2(4mn−3(n+m)+2)= =mn(mn−9)+6(m+n)−4 // n wierszy, m kolumn mn(mn−1) // wszystkie możliwe ustawienia 2 królów −2* // razy 2, bo dalej liczymy pola sąsiadujące, więc króle można zamienić miejscami m(n−1) // w każdej kolumnie mamy (n−1) sąsiadujących pionowo pól n(m−1) // w każdym wierszu mamy (m−1) sąsiadujących poziomo pól (m−1)(n−1) // pól sąsiadujących na ukos ↗↙ (m−1)(n−1) // pól sąsiadujących na ukos ↘↖ https://www.wolframalpha.com/input/?i=mn(mn-9)%2B6(m%2Bn)-4+where+n%3D8,+m%3D8 https://www.wolframalpha.com/input/?i=table%5Bmn(mn-9)%2B6(m%2Bn)-4,%7Bn,1,10%7D,%7Bm,1,10%7D%5D