1.Znajdź wszystkie liczby naturalne n, dla których liczba n^4+ 4 jest pierwsza. alinka: 1.Znajdź wszystkie liczby naturalne n, dla których liczba n⁴+ 4 jest pierwsza. odpowiedź uzasadnij. 2. Niech k będzie liczbą całkowitą. Wykaż że liczba 4k jest różnicą kwadratów dwóch liczb całkowitych. 3. Funkcja liniowa f spełnia warunki: f (1 ) =3 i f (3 ) = 1 . Oblicz f (4 ). 4. Pewien kwadrat i półkole mają równe obwody. Która z tych figura większe pole? 5. Wykaż, że przekątne równoległoboku dzielą się na połowy.

Benny: 1. n⁴+4=(n²+2−2n)(n²+2+2n)

Adam0: (k+1)²−(k−1)²=4k

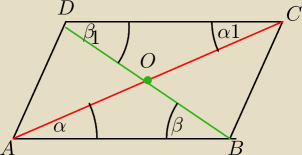
Krzysiek60: Nr 5 Ac i BD to przekatne rownolegloboku O − punkt przeciacia sie przekatnych rownolegloboku Teza AO= OC BO=OD Rozpatrzmy dwa trojkaty AOB i COD Trojkaty te maja AB= CD jako przeciwlegle boki rownolegloboku ∡α=∡α₁ ∡β= ∡β₁ jako katy naprzemianlegle wewnetrzne Na podstawie cechy przystawania trojkatow KBK stwierdzamy ze ΔAOB≡ΔCOD wobec czego AO= OC BO=OD Z tych rownosci wnioskujemy ze punkt O podzielil kazda z przekatnych na polowy . Wiec ustalamy jedna z wlasnosci rownolegloboku (jest ich kilka ) Twierdzenie : W rownolegloboku przekatne dziela sie na polowy

karty do gry : 3. :

f(3) − f(1)		f(4) − f(3)
	=
3 − 1		4 − 3

g: 1. n=1, n⁴+4 = 5. Z postu Bennego widać że n=1 to jedyne rozwiązanie.