czworokąt mat18: Mam jeszcze takie zadanie,którego nie potrafię ruszyć W czworokącie wypukłym ABCD na bokach AB i AD wybrano odpowiednio punkty E i F tak,że czworokąt AECF jest równoległobokiem Odcinki BF i ED przecinają się w punkcie M Wykaż,że czworokąty AEMF i BCDM mają równe pola pomoże ktoś? bardzo byłbym wdzięczny

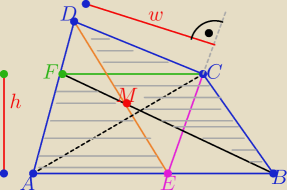
Eta: 1/ przejrzysty rysunek zgodnie z treścią zadania 2/ trójkąty ABF i ABC mają równe pola bo mają wspólną podstawę AB i wysokość "h" tej samej długości bo AB ∥FC ( z własności równoległoboku analogicznie trójkąty AEC i ECD też mają równe pola bo mają wspólną podstawę EC i wysokość "w" o tej samej długości bo AC∥AD zatem: P(AEMF) +P(EBM)=P(ABC)=P(AEC)+P(EBC)= P(ECD)+P(EBC)=P(EBCD)= P(BCDM)+P(EBM) czyli P(AEMF)=P(BCDM) ================ c.n.w