Rysowanie wykresu funkcji spełniającej warunki Andrzej: Witam, mam problem z rysowaniem wykresu funkcji spełniającego pewne warunki. Np. taki, że: − jest funkcją parzystą, − w x=−5 jest ciągła i nieróżniczkowalna, −w x=−2 ma asymptotę pionową tylko jednostronną, − w x=0 maksimum właściwe lokalne, −w x=4 ma punkt nieciągłości I rodzaju, −w x=6 ma punkt nieciągłości II rodzaju i jest prawostronnie ciągła. Jak się zabierać za tego typu zadania? Od czego zacząć? Posiada ktoś może link do efektywnej nauki tego typu zadań?

Blee: Przypomnij mi czym jest nieciaglosc I i Ii rodzaju

Andrzej: I rodzaju jeśli granice z obydwóch stron są skończone, a II jeśli jedna nie jest skończona

Blee: Nie wiem czy sa jakies strony ... musisz po prostu wyobrazic sobie jak moze wygladac ta funkcja. Skoro jest parzysta to wszystko co sie dzieje 'po prawej stronie' dzieje sie takze po lewej i na odwrot. Zaczynasz rysowac od x=0 ustawiasz sobie jakas wartosc po czym rysujesz luk zmierzajacy do dolu ... w x=2 zaznaczasz asymptote a wykres funkcji niech darzy do −∞ z lewej strony. Funkcja nie przyjmuje wartosci dla x=2 (kółko na jakies wartosci stawiasz) i od niego rysujesz dalej do x=4 gdzie masz asymptote kolejna odpowiednio wykres leci do ktorejs nieskonczonosci i z niej sie tez zaczyna I leci do x=5 gdzie masz OSTRY skok kata funkcji (jak np w |x| w zerze) i lecisz do x=6 gdzie funkcja z lewej strony przyjmuje jakas skonczona wartosc (kółko zamalowane) Rysujesz asymptote i z prawej strony lecisz z ktorejs nieskonczonosci i funkcja 'gdzies tam' sobie biegnie Teraz tylko odbijasz to przez os OX i masz przykladowy wykres funkcji spelniajacej takie warunki. Pisze z komorki wiec nie moge Ci tego narysowac.

Blee: Ale Mila na pewno Ci cos narysuje

Andrzej: no tak, ale funkcja ma asymptotę pionową tylko jednostronną w punkcie x= −2 a nie x=2, więc jest to różnica w rysowaniu jak jest parzysta? czy moge sobie po prostu −2 zamienic na 2?

Blee: Czy ty rozumiesz ze skoro jest parzysta to wszystko co jest dla x=−2 jest takze dla x=2 a dla x=4 jak cos jest to i jest dla x=−4

Andrzej: ok dzieki postaram sie ogarnąć

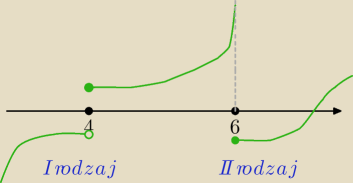
iteRacj@: na rysunku jest funkcja która w x=4 ma punkt nieciągłości I rodzaju, a w x=6 ma punkt nieciągłości II rodzaju i jest prawostronnie ciągła.

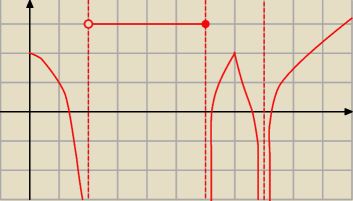
kochanus_niepospolitus: tu masz przykład takiej funkcji ... i to 'odbijasz' symetrycznie względem osi OX i już masz tylko mi się 'przesunęło za daleko to x=4

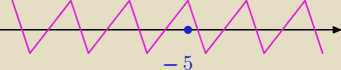
iteRacj@: ta jeszcze będzie ładna (jak teksańska piła mechaniczna) w x=−5 i nie tylko jest ciągła i nieróżniczkowalna

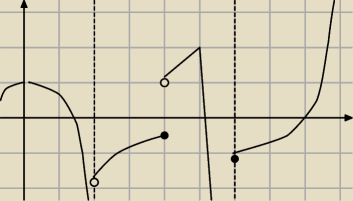
Andrzej: coś takiego narysowałem (oczywiście odbicie jest po lewej stronie), czy popełniłem gdzieś jakiś błąd? I jak to jest z tą nieróżniczkowalną, ona ma być taka szpiczasta tylko przez chwile czy jak?

iteRacj@: punktem z nieróżniczkowalnością jest oczywiście każdy pojedyńczy szpic i to wystarczy, ja narysowałam piłę z wieloma punktami i nie pomyslałam, że to może zaciemnić obraz

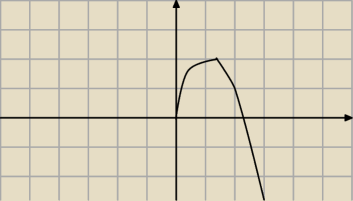
Andrzej : Czyli taki kawałeczek na przykład wystarczy?

iteRacj@: w zadaniu mamy: funkcja w x=−5 jest ciągła i nieróżniczkowalna, (u Ciebie jest to punkt o innej odciętej), ale z treści wynika, że f(x) ma spełniać te warunki tylko w tym punkcie, a dziedziną nie musi być ℛ, więc taki rysunek spełnia zadane warunki