Zadanie z parametrem
Filip: znajdź zbiór wszystkich parametrów a,b,c takich że parabola o równaniu y=ax2 +bx+c ma styczną
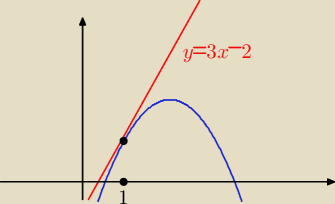
y=3x−2 w punkcie o pierwszej współrzędnej 1.
2 lut 10:16
Blee:
1) a>0
2) parabola przechodzi przez punkt (1,1) czyli a+b+c = 1
3) ze wzoru na styczna wynika ze f'(1) = 3 czyli 2a+b = 3
Czyli wszystkie parabole postaci f(x) = ax2 + (3−2a)x + (2+a) beda mialy taka styczna jezeli
tylko a>0
2 lut 10:29
Blee:
Na koncu mialo byc (−2+a) a nie (2+a)

2 lut 10:30
Filip: To wiem, ale da się jakoś wyznaczyć te wartości dla parametrów czy trzeba to zostawić w takiej
postaci?
2 lut 10:44
Blee:
Masz w zadaniu: podaj ZBIOR WSZYSTKICH parametrow. Co sugeruje ze to nie bedzie pojedyncza
'trojka' parametrow
2 lut 10:48
iteRacj@:
 Blee
Blee dlaczego trzeba odrzucić taką sytuację?
2 lut 10:48
Blee:
Bo głąb jestem

2 lut 10:55
iteRacj@:
i mam jeszcze jedną wątpliwość: w treści zadania mowa o punkcie o pierwszej współrzędnej 1
ale nie wiem dlaczego druga współrzędna tego punktu też wynosi 1
2 lut 10:56
iteRacj@:
z odpowiedzią z 10:55 się nie zgadzam
2 lut 10:57
Blee:
Skoro pierwsza wspolrzedna jest 1 to sprawdzamy wartosc stycznej w x=1 i otrzymujemy: y = 3 − 2
= 1
Piczatkowo mialem to ladnie rozpisane ale przez przypadek cofnalen strone i sie wkurzylem, a na
komorce za szybko sie nie pisze wiec olalem rozpisywanie
2 lut 10:59
iteRacj@: jasne, już wiem
2 lut 11:01

 Blee dlaczego trzeba odrzucić taką sytuację?
Blee dlaczego trzeba odrzucić taką sytuację?
