okrąg wpisany i opisany Partycja: Środek okręgu wpisango w trapez prostokątny znajduje się w odległości 24 i 32 od końców dłuższego ramienia trapezu. Oblicz pole trapezu.

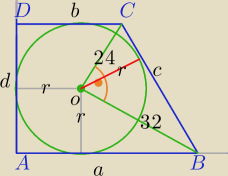
Mila: 1) c²=24²+32²=1600 c=40

	1
PΔCOB=		*24*32=384
	2

	1
PΔCOB=		*c*r
	2

1
	*40*r=384
2

20r=384 r=19.2 2) h=d=2*19.2=38,4 a+b=h+c=38,4+40

	78.4
PABCD=		*38.4
	2

Partycja: dzięki wielkie

Satan: Milu, mogłabyś mi powiedzieć skąd wniosek, że Δ_BOC jest prostokątny? Jakieś zaćmienie mam

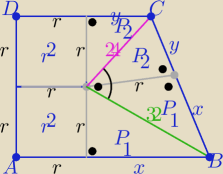
Eta: x+y= √24²+32²= 40 P(ABCD) = 2r²+2P₁+2P₂ =2r²+rx+ry = 2r²+r(x+y) = 2r²+40r=2r(r+40)

	24*32
r=		= .....
	40

P=..............

Mila: Satan Patrz na rysunek 21:53 ∡B+∡C=180 środek okręgu wpisanego w trapez leży na przecięciu dwusiecznych kątów wewnętrznych

1		1
	*|∡B|+		|∡C|)=90o
2		2

∡COB=90^o z sumy katów w ΔCOB

Eta: Janek ?

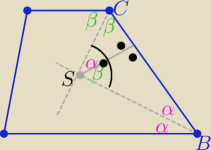
Eta: 2α+2β=180^o ⇒ α+β=90^o wniosek......

Satan: Milu, tak coś myślałem, ale lepiej się upewnić. Dziękuję