Planimetria Partycja: Trójkąt ABC jest równoboczny. Na boku BC obrano punkt D oraz przedłuzono bok AC do punktu E tak, że AD=DE. Wykaż, że BD=CE.

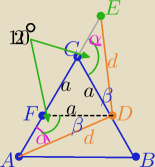
Eta: 1/ rysunek 2/ dorysowuję odcinek FD ∥AB to ΔFDC jest równoboczny o boku a 3/ trójkąt ADE jest równoramienny o ramionach d ( z treści zadania to kąty α mają równe miary 3/ w trójkątach ADF i CDE kąty AED i ECD mają też równe miary po 120^o zatem te trójkąty są przystające z cechy( bkb) więc |AF|=|CE| 4/ trapez ABDF jest trapezem równoramiennym ( bo ma równe kąty przy podstawie AB po 60^o co oznacza ,że |AF|=|BD|=|CE| co kończy dowód