trójkąt na płaszczyźnie kartezjańskiej Miniglef: Trójkąt ABC w którym |AC|=|BC| i znamy jego dwa punkty A=(2,3) i B=(5,4) jest równoramienny. Oblicz współrzędne wierzchołka C tego trójkąta wiedząc, że wierzchołek C leży na: a) osi x b) osi y

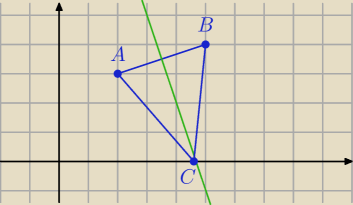
Janek191: a) Środek odcinka AB S = ( 3,5 ; 3,5) Prosta AB

	4 − 3		1
a =		=
	5 −2		3

	1
y =		x + b
	3

	1		1		7
3 =		*2 + b ⇒ b = 2		=
	3		3		3

	1		7
y =		x +
	3		3

Prosta prostopadła przechodząca przez S: y = − 3 x + k S = ( 3,5 ; 3,5) 3,5 = −3*3,5 + k 14 = k y = −3 x + 14 oraz y = 0 −3 x + 14 = 0 −3 x = − 14

	14		2
x =		= 4
	3		3

	2
C = ( 4		, 0)
	3

===============

Janek191: b) y = −3 x + 14 x = 0 więc y = 14 C = ( 0, 14) ============

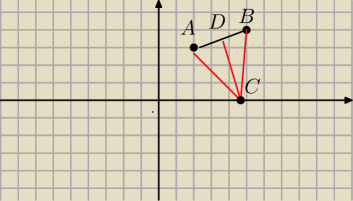
Krzysiek60: a) wierzcholek C na osi OX napisac rownanie wysokosci CD i jej punkt przeciecia z osia OX wyznaczy wierzcholek C To jest szkic do zadania (nie dokladny rysunek ) ma pokazac o co kaman

Janek191: Pozdrowienia dla Krzyśka60:

Miniglef: Ok, a czy mogę w obu przypadkach skorzystać ze wzoru na długość odcinka AC i BC i to co mi wyjdzie do siebie przyrównać? W tym wypadku w punkcie otrzymałam: a) xc=4 i 2/3, czyli razem wierzchołek C=(4 i 2/3, 0) b) yc=4, czyli razem wierzchołek C= (0,4)

Krzysiek60: Dobry wieczor Janek191 Pozdrawiam rowniez

Janek191: a) Tak b) Nie może być y_c = 4

Krzysiek60: w b) nieprawda ze dla C=(0.4) AB=BC

Miniglef: A poprawka, tym moim sposobem wyszło mi w punkcie b yc = 14. Czyli inny sposób, ale wynik jak u Ciebie dziękuję bardzo!

Janek191: a) C = ( x, 0) I AC I² = I BC I² b) C = ( 0, y) I AC I² = I BC I² y = 14

Miniglef: tak, tak właśnie zrobiłam od razu i wydaje mi się, ze jest to lepszy sposób, bo krótszy i łatwiej go wytłumaczyć. Tylko w obliczeniach się pomyliłam i zamiast 14 miałam 4. Ale jest git

Janek191: