Cwiczenie nr 5 Krzysiek60: Wypisz 5 pierwszych wyrazow ciagu (S_n) z definiowanego indukcyjnie S₀=0 S_n+1= S_n+(n+1) czy umiesz znalezc recepte na szukanie S_n?

Adam0: S_n − suma ciągu arytmetycznego o różnicy 1

	(n+1)n
Sn=
	2

Krzysiek60: Adam ciagow arytnetycznych nie bylo jescze

Adam0: S_n=1+2+...+(n−1)+n=n+(n−1)+...+2+1 S_n+S_n=(1+n)+(2+(n−1))+...+((n−1)+2)+(n+1)=(n+1)*n

	n(n+1)
Sn=
	2

Krzysiek60: Adam byc moze tak jest tak jak piszsesz ale ja musze robic to cwiczenie tak jak mam w tresci Inaczej tego nie zrozumie .

Krzysiek60: S₀=0 S₁= S₀+(0+1) = S₀+1 S₂= S₁+(1+1)= S₁+2 S₃= S₂+(2+1)= S₂+3 S₄= S₃+(3+1)= S₃+4 Milu cwiczenie nr 5 strona 91

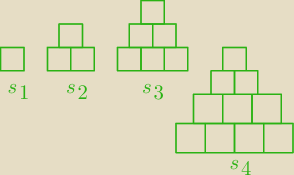
Mila: s₀=0 s₁=0+(0+1)=1 s₂=1+(1+1)=3 s₃=3+ (2+1)=6 s₄=6+(3+1)=10 s₅=10+(4+1)=15 To są kolejne liczby trójkątne. Każdy wyraz ciągu odpowiada liczbie klocków w pewnej piramidzie. s₄ −w podstawie 4 klocki , liczba klocków w piramidzie.

	1
4+3+2+1= (4+1)+(3+2)=2*5=		*4*(4+1)
	2

	1
sn=		*n*(n+1)
	2

	1
s5=		*5*(5+1)=15
	2

Krzysiek60: Dziekuje Ci bardzo Juz jutro to rozkimam

Mariusz: Krzysiek jak ci się podobają funkcje tworzące ? G(x)=∑_n=0^∞S_nxⁿ

	xn
E(x)=∑n=0∞Sn
	n!

Tutaj lepiej będzie pasować funkcja G(x)