Uzasadnij, że pole trójkąta ABC jest największe
Oxydos: Punkty A i B leżą na krzywej o równaniu x2−y+1=0 i są symetryczne względem punktu M=(−1,4) i
wraz z punktem C leżącym na krzywej pomiędzy punktami A i B wyznaczają trójkąt. Uzasadnij, że
pole trójkąta ABC jest największe, jeśli C=(−1,2). Proszę o odpowiedź
1 lut 14:14
===:
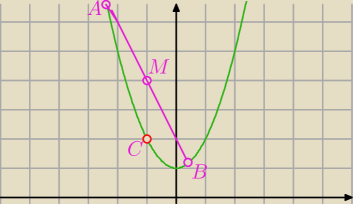
Moze i jest łatwiejszy sposób ... na pierwszy rzut widzę taki:
Współrzędne punktów A i B ustalisz z wykorzystując wzór na współrzędne środka odcinka.
Napiszesz równanie prostej przez punkty A i B
Poszukasz współrzednych punktu C tak aby odleegłość tego punktu od prostej była największa
(ale punkt leżał na danej krzywej pomiędzy A i B)
1 lut 15:28
===:
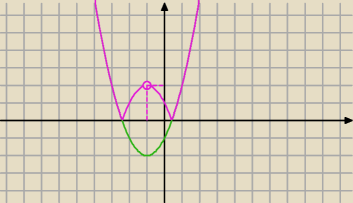
Sprowadzi się to do znalezienia f(c)
max|x
c2+2x
c−1|
w przedziale <−1−
√2, −1+
√2>
1 lut 15:44
 Moze i jest łatwiejszy sposób ... na pierwszy rzut widzę taki:
Współrzędne punktów A i B ustalisz z wykorzystując wzór na współrzędne środka odcinka.
Napiszesz równanie prostej przez punkty A i B
Poszukasz współrzednych punktu C tak aby odleegłość tego punktu od prostej była największa
(ale punkt leżał na danej krzywej pomiędzy A i B)
Moze i jest łatwiejszy sposób ... na pierwszy rzut widzę taki:
Współrzędne punktów A i B ustalisz z wykorzystując wzór na współrzędne środka odcinka.
Napiszesz równanie prostej przez punkty A i B
Poszukasz współrzednych punktu C tak aby odleegłość tego punktu od prostej była największa
(ale punkt leżał na danej krzywej pomiędzy A i B)
 Sprowadzi się to do znalezienia f(c)max|xc2+2xc−1|
w przedziale <−1−√2, −1+√2>
Sprowadzi się to do znalezienia f(c)max|xc2+2xc−1|
w przedziale <−1−√2, −1+√2>