przedział całkowania
Donald : ∫∫ x+y dxdy po obszarze D. D jest trójkątem o współrzędnych A=0,0 B=3,0 C=3,6. Jaki przedział
całkowania ma być?
1 lut 08:39
jc: To całka podwójna. Całkujemy po trójkącie, nie po przedziale.
1 lut 08:49
Donald : dobrze więc jaka ma być granica całkowania?
1 lut 08:51
Donald : no jak to będzie?
1 lut 09:03
jc: Zwyczajnie.
∫03 dx ∫02x (x+y) dy
1 lut 09:03
Donald : czemu 2x?
1 lut 09:08
Donald : myślałem, że powinno być x?
1 lut 09:24
Donald : dlaczego zamiast x jest 2x?
1 lut 09:41
Mila:
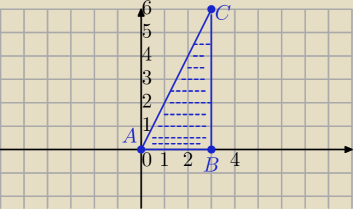
1)
0≤x≤3
Prosta AC: y=2x
0≤y≤2x
∫
03 [∫
02x (x+y) dy] dx
1 lut 15:00
Lech: Sprawdz rownanie prostej AC : y= 2x .
Zrob rysunek tego trojkata i zobaczysz granice calkowania : 0 ≤ x ≤ 3 , 0 ≤ y ≤ 2x
i wykonaj calkowanie jak podal @jc.
1 lut 15:04
Donald: wychodzi mi 18, a powinno 36 nie wiem co jest źle. Mógłby to ktoś przeliczyć? Dzięki za
wyjaśnienie, zrozumiałem ten obszar całkowania
1 lut 19:33
Mila:
∫
03 [∫
0y=2x (x+y) dy] dx=
| | 1 | |
=∫03([(xy+ |
| y2]0y=2x)dx= |
| | 2 | |
| | 1 | | 1 | |
=∫03(x*2x+ |
| *(2x)2−x*0− |
| *0)dx= |
| | 2 | | 2 | |
| | 1 | |
=∫03(2x2+2x2)dx=∫03(4x2)dx=[4* |
| x3]03= |
| | 3 | |
| | 4 | | 4 | |
= |
| *33−0= |
| *27=4*9=36 |
| | 3 | | 3 | |
1 lut 20:02
Donald: Dziękuje! Mila
1 lut 20:13
Mila:
1 lut 20:15