algebra algebra: Liczę argument α liczby −1+i.

	√2		√2
Wychodzi na to, że cosα = −		, a sinα =
	2		2

i teraz nie pamiętam co się robiło, gdy wychodziła ujemna (w tabeli wartości funkcji trygonometrycznych są same nieujemnie wartości) Proszę o pomoc.

Maciess: Jak chodzi o α to kąt to z drugiej ćwiartki (tam sin jest dodatni a cos ujemny) czyli α

	3π
	4

Mila:

	√2		π
cosα=		⇔α=		− kąt ostry z I ćwiartki
	2		4

cosα<0 i sinα>⇔kąt α z II ćwiartki

	π		3π
α=π−		=
	4		4

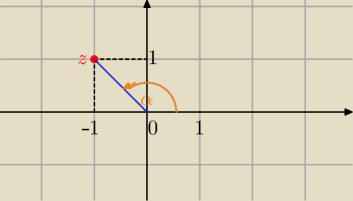
albo geometrycznie (−1,1) na płaszczyźnie zespolonej

algebra: Rozumiem, dziękuje Wam za pomoc