wykaż mat: W trapez ABCD wpisano okrąg o środku O i promieniu r

	1		1		1		1
Wykaż,że		+		=		+
	|AO|2		|DO|2		|BO|2		|CO|2

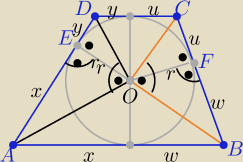Eta: 1/ rysunek 2/ z warunku wpisania okręgu w trapez trójkąty ADO i BCO są prostokątne w ΔADO i w ΔBCO r²=xy r²=wu i z tw. Pitagorasa |AO|²= r²+x² i |BO|²=r²+w² |DO|²= r²+y² i |CO|²=r²+u² |AO|²=xy+x²=x(y+x) i |BO|²= wu+w²=w(u+w) |DO|²= y(y+x) i |CO|²= u(u+w) to

1

1

1

1

y+x

1

1

+

=

+

=

=

=

|AO|2

|DO|2

x(x+y)

y(x+y)

xy(x+y)

xy

r2

i podobnie :

1		1		1		1
	+		=............. =		=
|BO|2		|CO|2		uw		r2

zatem taka równość zachodzi c.n.w.