funkcje, dowody dominiqe: Udowodnij, że jeśli f jest rosnąca i f≥0 , to funkcja f² też jest rosnąca. i, trochę wg mnie trudne, z tym na górze to jeszcze się da, bo tam można chyba wykorzystać pochodne. ale tu jest bomba: Podaj przykład rosnącej funkcji f, takiej, że f² jest malejąca.

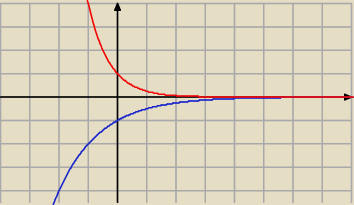
PW: Zakładamy, że f jest rosnąca i różniczkowalna oraz f'(x)>0 (f²(x))'=2f(x)f'(x)<0⇔f(x)<0 − funkcja f musi być ujemna w całej dziedzinie (ujemna i rosnąca).

PW:

PW: A co do pierwszego problemu − nie można korzystać z pochodnej, bo nie ma założenia różniczkowalności funkcji f.

dominiqe: w takim razie jak to pierwsze uszczknąć?

dominiqe: hm? Pomoże ktoś?

PW: A zwyczajnie, przy założeniu że f jest rosnąca i dla wszystkich x dodatnia^*) − Jeżeli f(x₁)<f(x₂), to f(x₁)f(x₁)<f(x₂)f(x₁)<f(x₂)f(x₂). _{−−−−−−−−−−−−} ^*)Warunek f(x)≥0 podany dla funkcji rosnącej jest śmieszny − to gdzie ona miałaby przyjmować wartość 0?