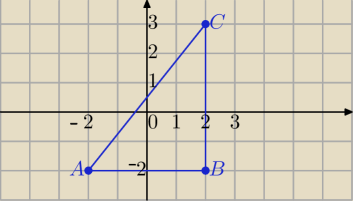
Całka podwójna Timon i Pumba: Obliczyć całkę podwójną ∬2dxdy, gdzie D jest trójkątem o wierzchołkach D (−2,−2), (2,3), (2,−2) i podać jej interpretacje geometryczną. Czy ktoś mógłby mi ją rozwiązać krok po kroku? Kompletnie nie wiem jak to liczyć.

Mila: 1) _D∫∫2dxdy=.. Granice stałe: −2≤x≤2 granice zmienne:

	5		1
prosta AC: y=		x+
	4		2

prosta AB: y=−2

	5		1
−2≤y≤		x+
	4		2

=2*₋₂∫²[₋₂∫^(5/4)x+(1/2)dy]dx= pierwsze całkowanie w granicach zmiennych, drugie w granicach stałych =2*₋₂∫²[y]₋₂^(5/4)x+(1/2) dx=

	5		1		5		1
=2*−2∫2[		x+		−(		*(−2)+		)]dx=
	4		2		4		2

	5		5
=2*−2∫2(		x+		) dx=
	4		2

	5		1		5
=2*[		*		x2+		x]−22}=
	4		2		2

	5		5		5		5
=2*[		*4+		*2−(		*4+		*(−2)]=2*10=
	8		2		8		2

=20 2) Podwojone pole trójkąta ABC.

Ametyst: Ślicznie dziękuje za rozwiązanie, teraz rozumiem jak to liczyć