 Pozdrawiam...
Pozdrawiam...
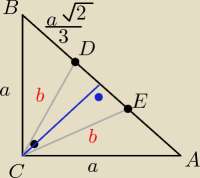 z twierdzenia cosinusów
z twierdzenia cosinusów
| a√2 | ||
( | )2 = b2 + b2 − 2b2 * cosα
| |
| 3 |
| 2a2 | |
= 2b2 − 2b2cosα
| |
| 9 |
| 2a2 | |
= 2b2(1−cosα)
| |
| 9 |
| a2 | |
= 1−cosα
| |
| 9b2 |
| a2 | ||
cosα = 1− | ||
| 9b2 |
| a√2 | |
)2 + h2 = b2
| |
| 3 |
| a2 | ha√2 | |||
P = | = | |||
| 2 | 2 |
| a | ||
h= | ||
| √2 |
| a√2 | a2 | ||
)2 + | = b2
| ||
| 6 | 2 |
| 2a2 | a2 | ||
+ | = b2
| ||
| 36 | 2 |
| a2 | 9a2 | ||
+ | = b2
| ||
| 18 | 18 |
| 10a2 | |
= b2
| |
| 18 |
| √180a | 6√5a | a√5 | ||||
b= | = | = | ||||
| 18 | 18 | 3 |
| a2 | 1 | 9 | 1 | 4 | ||||||
cosα = 1− | = 1 − a2 * | * | = 1− | = | ||||||
| 9b2 | 9 | 5a2 | 5 | 5 |
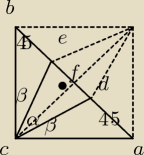 A=a, B=b, C=c, D=d, E=e ,F=f
AB=AC√2 , DE=AC√2:3, EF=AC√2:6 , CF= AC√2:2, z tw. Pitagorasa dlaΔCFE→CE2=CF2+EF2
→CE=√5AC:3
cos12α=CF:CE=(AC√2:2):(AC√5:3)
A=a, B=b, C=c, D=d, E=e ,F=f
AB=AC√2 , DE=AC√2:3, EF=AC√2:6 , CF= AC√2:2, z tw. Pitagorasa dlaΔCFE→CE2=CF2+EF2
→CE=√5AC:3
cos12α=CF:CE=(AC√2:2):(AC√5:3)
 Wynik poprawny , ale można prościej
Wynik poprawny , ale można prościej  IAEI= x , x >0
to ICFI= 32x ( bo Δ CAF prostokatny i równoramienny o ramieniu 32x
ICEI=ICDI
ICEI2 = (32x)2 + (x2)2= 104x2
IAEI= x , x >0
to ICFI= 32x ( bo Δ CAF prostokatny i równoramienny o ramieniu 32x
ICEI=ICDI
ICEI2 = (32x)2 + (x2)2= 104x2
| x√10 | ||
ICEI= | ||
| 2 |
| ICEI2+ICDI2 − IDEI2 | 5x2 −x2 | 4 | ||||
cos< DCE = | = | = | ||||
| 2*ICEI*ICDI | 5x2 | 5 |