Proste PA i PB są styczne do okręgu o środku w punkcie O w punktach A i B. Prost alinka: Proste PA i PB są styczne do okręgu o środku w punkcie O w punktach A i B. Prosta KL jest styczna do tego okręgu w punkcie C i przecina PA i PB odpowiednio w punktach K i L. oblicz obwód trójkąta PKL, iwedząc, że |PA|= 2012 a |KL|=2011. Rozważ wszystkie przypadki. odpowiedź uzasadnij. przedstaw wszystkie obliczenia.

Eta: No to choć raz ... alinko przedstaw , uzasadnij i podaj obliczenia bo matura zbliża się wielkimi krokami

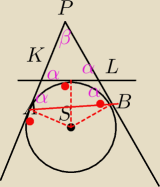
alinka: Nie ma pojęcia jak to wynoać mam jedynie rysunek i to PA= PB = 2012 czyli ΔPKL jest równoramienny. i Δpkl jest podobny do Δpab

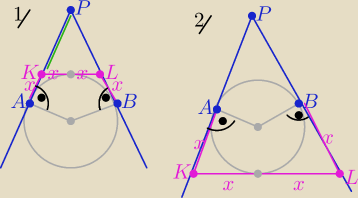
Eta: 1/ Z twierdzenia o odcinkach stycznych |KL|=2x =2011 i |KP|=|LP|=2012−x Obwód ΔKLP = 2*|KP| +|KL|=............... 2/ analogiczne ... z tym,że |KP|=|LP|=x+2012 i |KL|=2x= 2011 Obwód Δ KLP = 2*|KP| +|KL|=.............

Alinka: O dziękuję bardzo 💕

Eta: