wykaż że
Estefan: Wykaż, że jeśli liczby a i b są nieujemne, to (a2 + b2)/2 ≥ [(a+b)/2]2
30 sty 21:44
Eta:
To nierówność między średnią kwadratową a średnią arytmetyczną

30 sty 21:50
Eta:
(a−b)
2≥0⇔ a
2+b
2≥2ab / +a
2+b
2
2a
2+2b
2≥ a
2+2ab+b
2 /:4
c.n.w
30 sty 21:55
Estefan: dziękuję
30 sty 22:08
Eta: 
30 sty 22:09
jc:
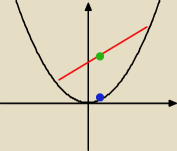
a i b mogą być dowolne. Nierówność mówi, że funkcja kwadratowa jest wypukła.
Niebieska kropa leży pod zieloną.
30 sty 22:21


 a i b mogą być dowolne. Nierówność mówi, że funkcja kwadratowa jest wypukła.
Niebieska kropa leży pod zieloną.
a i b mogą być dowolne. Nierówność mówi, że funkcja kwadratowa jest wypukła.
Niebieska kropa leży pod zieloną.