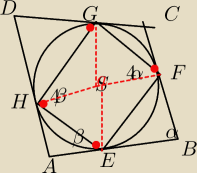
Okrąg o promieniu długości r (r>0) jest wpisany w czworokąt wypukły ABCD. Okrąg alinka: Okrąg o promieniu długości r (r>0) jest wpisany w czworokąt wypukły ABCD. Okrąg ten jest styczny do boków AB, BC, Cd, DA odpowiedniu w punktach E,F,G i H. wiadomo, że ∡EHG = 4 ∡BEF, ∡EFG= 4 ∡AEH Wówczas wyznacz HF − lub zapisz nierówność dla HF, względem r i √3 odpowiedź uzasadnij.

alinka: Up

alinka: Up

Satan: W czym problem? Wykorzystaj warunek na wpisanie okręgu w czworokąt oraz odcinkach stycznych.

alinka: wałsnie mi nic nie wychodzi

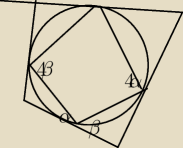
alinka: pomoże ktoś mam tyle: i α+β=45

Qulka: ooo a myślałam że potrafisz pisać tylko uzasadnij ..a jednak czasem coś tu namalujesz więc ten kąt na górze ma 45° (bo ten na dole 135°) więc środkowy opaty na HF ma 90° więc HF=r√2