Dane są dwa okręgi: pierwszy o środku w punkcie o i promieniu R, drugi o środku
alinka: Dane są dwa okręgi: pierwszy o środku w punkcie o i promieniu R, drugi o środku S i promieniu r
(R>r>0) styczne zewnętrznie w punkcie A. Do tych okręgów poprowadzono wspólną styczną
zwenętrznie BC niezawierającą punktu a, gdzie B i C są punktami styczności odpowiedni do
okręgów o środku O i S. Oblicz pole pow. czworokąta BSC, długość BC. Odpowiedź uzasadnij
30 sty 21:18
Eta:
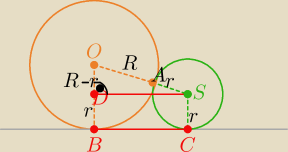
|OS|=R+r , |OD|=R−r , |BC|=|DS|
Z tw. Pitagorasa w ΔOSD
|DS|
2= (R+r)
2−(R−r)
2 = ....... = 4Rr
to |DS|=|BC|= 2
√Rr [j]
==============
Czworokąt BOSC ( pewnie taki miał być ... zjadłaś literkę O
jest trapezem
| | R+r | |
P(trapezu BOSC) = |
| *2√Rr |
| | 2 | |
P=(R+r)
√Rr [j
2]
===========
30 sty 21:46
alinka: dziękuję
30 sty 21:52
Eta:

30 sty 21:56
 |OS|=R+r , |OD|=R−r , |BC|=|DS|
Z tw. Pitagorasa w ΔOSD
|DS|2= (R+r)2−(R−r)2 = ....... = 4Rr
to |DS|=|BC|= 2√Rr [j]
==============
Czworokąt BOSC ( pewnie taki miał być ... zjadłaś literkę O
jest trapezem
|OS|=R+r , |OD|=R−r , |BC|=|DS|
Z tw. Pitagorasa w ΔOSD
|DS|2= (R+r)2−(R−r)2 = ....... = 4Rr
to |DS|=|BC|= 2√Rr [j]
==============
Czworokąt BOSC ( pewnie taki miał być ... zjadłaś literkę O
jest trapezem
