 b)
b)
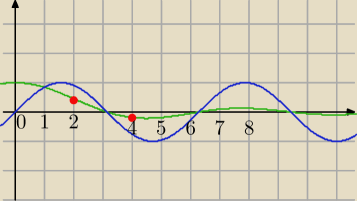
| 1 | sinx | |||
f(x)= | *sinx = | już Ci tłumaczyłam | ||
| x | x |
| 1 | ||
limx→∞ | =0 | |
| x |
 c)
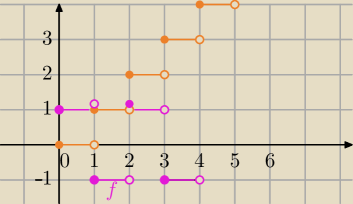
f(x)=(−1)[x]
f(x)=(−1)0=1 dla x∊<0,1)
f(x)=(−1)1=−1 dla x∊<1,2)
f(x)=(−1)2=1 dla x∊<2,3)
f(x)=(−1)3 =−1 dla x∊<3,4)
wniosek :
limx→∞ f(x) granica nie istnieje
c)
f(x)=(−1)[x]
f(x)=(−1)0=1 dla x∊<0,1)
f(x)=(−1)1=−1 dla x∊<1,2)
f(x)=(−1)2=1 dla x∊<2,3)
f(x)=(−1)3 =−1 dla x∊<3,4)
wniosek :
limx→∞ f(x) granica nie istnieje
| 1 | ||
limx→∞ | =0 | |
| x2 |
 Wiem ze kiedys tlumaczylas .ale to mi gdzies zginelo i poprosilem jescze raz o pmoc .
Wiem ze kiedys tlumaczylas .ale to mi gdzies zginelo i poprosilem jescze raz o pmoc .