Funkcja sgn(x)
Krzysiek60:
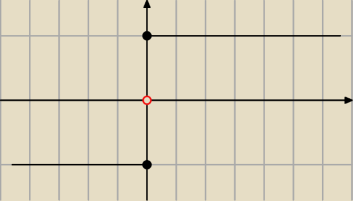
Czy tak wyglada wykres funcji f(x)= sgn(x) ?
30 sty 19:55
iteRacj@: dobry wieczór!
nie
30 sty 19:56
Pytający:
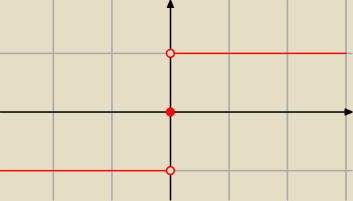
Nie.
30 sty 19:57
Pytający:
Dobry wieczór.

30 sty 19:57
iteRacj@: na tym rysunku argumentowi x=0 przyporządkowane są dwie wartości −1 i 1
30 sty 19:58
iteRacj@: na tym rysunku Krzysztofa
30 sty 19:58
iteRacj@:
Krzysztof, narysuj jeszcze np. g(x)= sgn(x2) albo sgn(x2−1)
30 sty 20:05
Krzysiek60:
Dobry wieczor
iteRacjo ]]

czesc
Pytajacy
Chcialem wyslac post ale koputer odmowil wspolpracy
Za chwile naprowadzisz mnie na te wykresy
Teraz jednak mam takie polecenie
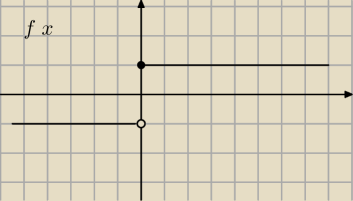
Do czego daza wartosci f(x) i g(x) gdy x zbliza sie do 0 z prawej strony jezeli f(x)=
Z prawej strony f(x) dazy do 1
g(x) dazy do 0 . czy dobrze ?
30 sty 20:14
Krzysiek60: natomiast polecenie 20 : 05 nie wiem ja wykonac .
30 sty 20:22
iteRacj@: dla g(x) = sgn(x) granica prawostronna w zerze wynosi 1, spójrz na rysunek z 19:57
| | x | |
dla f(x) = |
| granica prawostronna w zerze wynosi też 1 |
| | |x| | |
a jaka funkcja jest na rysunku z 20:14?
30 sty 20:28
Krzysiek60:
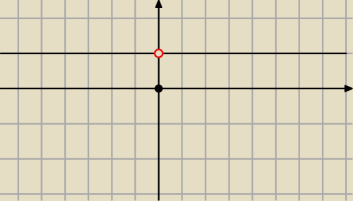
wedlug mnie tak g(x)= sgn(x
2)
30 sty 20:32
iteRacj@: yes!
30 sty 20:32
Krzysiek60: | | x | |
Post 20 : 14 to f(x)= |
| |
| | |x| | |
30 sty 20:34
iteRacj@: x=0 nie należy do dziedziny funkcji
30 sty 20:35
Krzysiek60:
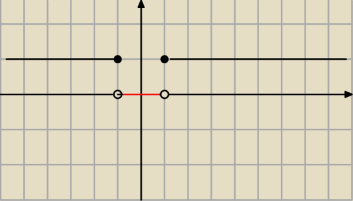
Tak bym narysowal g(x)=sgn(x
2−1)
30 sty 20:36
Krzysiek60:
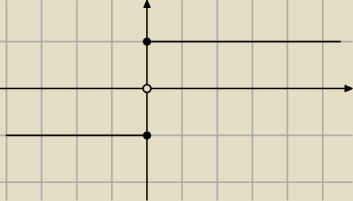
Wiec f(x) z 20 : 14
30 sty 20:38
iteRacj@:
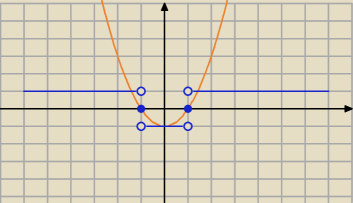 f(x)=x2−1
g(x)=sgn(x2−1)
f(x)=x2−1
g(x)=sgn(x2−1)
łatwiej się rysuje obie funkcje naraz
30 sty 20:42
iteRacj@:
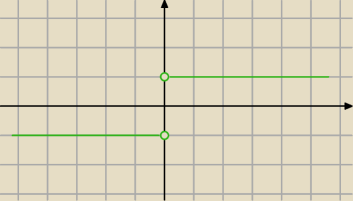
D=R−{0}
30 sty 20:44
Krzysiek60: To narysowalem odwrotnie
dziekuje CI za pomoc w tym poscie
30 sty 20:45
iteRacj@: promuję funkcję signum

30 sty 20:47
Krzysiek60: Wiem

30 sty 20:49
 Czy tak wyglada wykres funcji f(x)= sgn(x) ?
Czy tak wyglada wykres funcji f(x)= sgn(x) ?
 Nie.
Nie.

 Dobry wieczor iteRacjo ]]
Dobry wieczor iteRacjo ]]  czesc Pytajacy
Chcialem wyslac post ale koputer odmowil wspolpracy
Za chwile naprowadzisz mnie na te wykresy
Teraz jednak mam takie polecenie
Do czego daza wartosci f(x) i g(x) gdy x zbliza sie do 0 z prawej strony jezeli f(x)=
czesc Pytajacy
Chcialem wyslac post ale koputer odmowil wspolpracy
Za chwile naprowadzisz mnie na te wykresy
Teraz jednak mam takie polecenie
Do czego daza wartosci f(x) i g(x) gdy x zbliza sie do 0 z prawej strony jezeli f(x)=
 wedlug mnie tak g(x)= sgn(x2)
wedlug mnie tak g(x)= sgn(x2)
 Tak bym narysowal g(x)=sgn(x2−1)
Tak bym narysowal g(x)=sgn(x2−1)
 Wiec f(x) z 20 : 14
Wiec f(x) z 20 : 14
 f(x)=x2−1
g(x)=sgn(x2−1)
łatwiej się rysuje obie funkcje naraz
f(x)=x2−1
g(x)=sgn(x2−1)
łatwiej się rysuje obie funkcje naraz


