Hiperbole Krzysiek60:

	2x
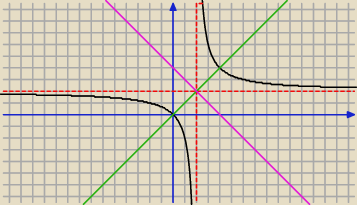
Narysujmy wykres funkcji f(x)=
	x−2

D_f= R\{2}

	2x		2x−4+4		2(x−2)		4		4
f(x)=		=		=		+		=		+2
	x−2		x−2		x−2		x−2		x−2

Znajdz osie symetrii tej funkcji Pierwsza osia symetrii bedzie prosta y=x Jeszcze bedzie druga os prostopadla do y=x i przechodzaca przez punkt (2,2) y= −1(x−2)+2= −x+4