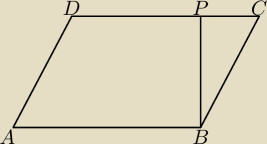
Woda: W rombie ABCD z wierzchołka B poprowadzono wysokość, która przecięła bok DC w punkt P. Wiedząc, że: ^|AC|+|DB|_|AC|−|DB|=7 udowodnij, że ^|PC|_|DP=⁷₁₈. Zrobiłem to w ten sposób, że |AC|=⁴₃|DB|, następnie wszystko obliczyłem na zmiennej x=|DB|, bok z tw. Pitagorasa, potem wysokość porównując dwa wzory na pole, potem z tw. Pitagorasa |DP| i |PC|, sprawdziłem czy w sumie daje to długość boku i dopiero potem proporcja |PC| do |DP| Da się to jakoś szybciej, tak z ciekawości?

Eta:

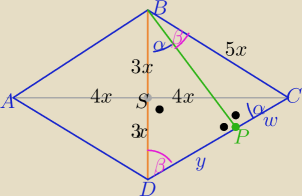
	f		8
1/ f+e=7f−7e ⇒ 6f=8e ⇒		=
	e		6

przekątne mają długości f= 8x i e= 6x , to długość boku rombu jest a= 5x =y+w 2/ z podobieństwa trójkątów BPD i DSC z cechy (kkk)

y		3x		18x
	=		⇒ y=
6x		5x		5

	7x		w		7
i w= 5x−y=		to		=
	5		y		18

Woda: dzieki

Eta: Na rys. sorry ( przy B niepotrzebnie wpisał mi się kąt β ( tam go nie ma