parametr Ukośnik: Dla jakich wartości parametru a równanie |x + a| = 1 − || x −2 | − 3| ma dokładnie 2 rozwiązania? Jakaś propozycja rozwiązania bez wykresu?

Ukośnik: ponawiam

Basia: Da się. Dość dużo pisania. Z komórki nie napiszę. I trochę szkoda czasu. Idea jest taka: dla x<2 mamy |x+a|=1−|2−x−3| |x+a|=1−|−1−x|=1−|x+1| czyli dla x<1 mamy |x+a|=1−(−x−1)=2+x sprzeczność bo dla x<2 2+x<0 dla x∊<1,2) mamy |x+a|=1−x−1=−x znowu sprzeczność tak samo dla x≥2 mogłam się pomylić, niewygodnie mi z tej komórki

Basia: drugiej sprzeczności nie ma może być |x+a|=0 x=−a jedno rozwiązanie dla a∊(−2,1>

Basia: Pierwszej też nie. Jednak komórka jest do kitu. Jutro Ci to pokażę jeżeli nikt się nie zlituje.

Ukośnik: Mam nadzieję, że ktoś się jednak zlituje, bo potrzebuję to na dzisiaj, a twoim sposobem mi nie wychodzi Ale dzięki za starania

Qulka: a czemu bez wykresu?

Qulka: a∊(−6;−4)u(0;2)

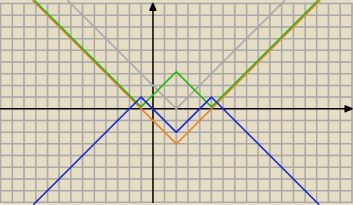
Qulka: prawa strona

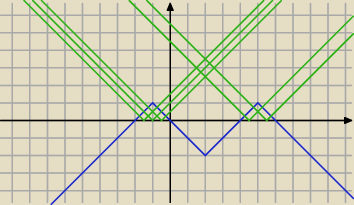
Qulka: zielone to a a∊(−6;−4)u(0;2)

Eta: Jak już chcesz algebraicznie to: aby równanie miało 2 rozwiązania to prawa strona musi być >0 −1||x−2|−3|>0 ⇒||x−2|−3|<1 ⇒ |x−2| <4 i |x−2|>2 x−2<4 i x−2>−4 i x−2>2 lub x−2< −2 x∊(−2,6) i x∊( −∞,0)u(4,∞) to x∊(−2,0) u(4,6) zatem |x+a| ma dwa rozwiązania gdy −a∊(−2,0) lub −a∊(4,6) ⇒ a∊(−6,−4)u(0,2) ===============

Ukośnik: A skąd się bierze − przed a?

Satan: Wartość bezwzględna ma postać |x − b|. Więc skoro mamy |x + a|, to tak naprawdę jest to |x − (−a)|

Eta:

Ukośnik: Bez wykresu, bo nie lubię wykresów Dzięki wszystkim za pomoc