 Cwiczenie nr 15 strona 78 klasa 2
Cwiczenie nr 14 zrobilem (tylko prosta y=−U{1}[x} jest hiperbola
Cwiczenie nr 15 strona 78 klasa 2
Cwiczenie nr 14 zrobilem (tylko prosta y=−U{1}[x} jest hiperbola
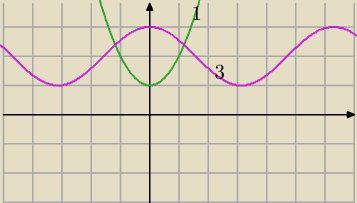 15)
np.
1)
f(x)=x2+1
f(|x|)=x2+1
2)
f(x)=x4+x2=f(|x|)
3)
f(x)= cosx+2
Wniosek sam napisz.
Napisz swoje propozycje.
15)
np.
1)
f(x)=x2+1
f(|x|)=x2+1
2)
f(x)=x4+x2=f(|x|)
3)
f(x)= cosx+2
Wniosek sam napisz.
Napisz swoje propozycje.
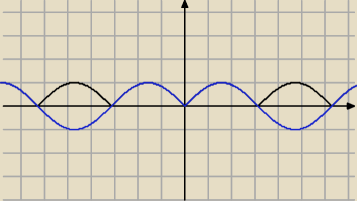 Milu
Dowiedzialem sie od === na czym polega ta funkcja f(|x|)
i np f(x)= |sin(x)|≠sin(\x\) jest inny wykres . Wiec ta rownosc nie zachodzi dla kazdej
funkcji
Moze tutaj chodzi o to zeby funkcja byla parzysta ?
Milu
Dowiedzialem sie od === na czym polega ta funkcja f(|x|)
i np f(x)= |sin(x)|≠sin(\x\) jest inny wykres . Wiec ta rownosc nie zachodzi dla kazdej
funkcji
Moze tutaj chodzi o to zeby funkcja byla parzysta ?
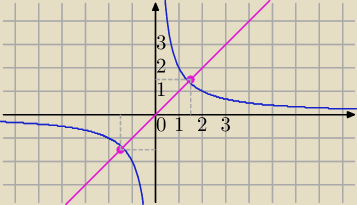 17)
17)
| a | ||
fa(x)= | i a>0 | |
| x |
| a | |
=x | |
| x |

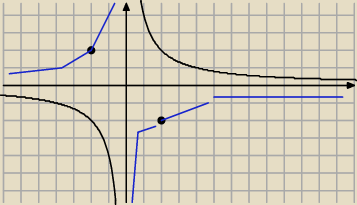 Juz Milu lepiej .
Cwiczenie nr 18
te niebieskie to obraz hiperboli w symetrii wzgledem osi OX
Jak nazwiesz funkcje ktorej wykres narysowales ?
Przypominamy ze wykres funkcji y= f(x−r)+s(y−s)= f(x−r) jest wynikiem przesuniecia wykresu y=
f(x) o wektor [r ,s]
O co tutaj Milu chodzi
W sumie taki sam wykres bedzie w symetrii wzgledem osi OY
Juz Milu lepiej .
Cwiczenie nr 18
te niebieskie to obraz hiperboli w symetrii wzgledem osi OX
Jak nazwiesz funkcje ktorej wykres narysowales ?
Przypominamy ze wykres funkcji y= f(x−r)+s(y−s)= f(x−r) jest wynikiem przesuniecia wykresu y=
f(x) o wektor [r ,s]
O co tutaj Milu chodzi
W sumie taki sam wykres bedzie w symetrii wzgledem osi OY
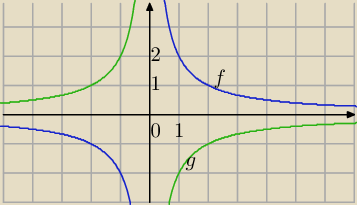 Komentarz jest do przesunięcia równoległego
1)
Wzór po przekształceniu wykresu funkcji
Komentarz jest do przesunięcia równoległego
1)
Wzór po przekształceniu wykresu funkcji
| 2 | ||
f(x)= | przez symetrię względem OX | |
| x |
| −2 | ||
g(x)= | ||
| x |
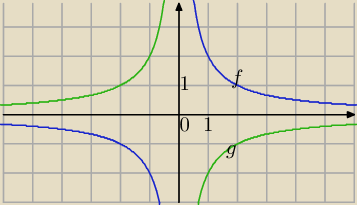 Wzór po przekształceniu wykresu funkcji
Wzór po przekształceniu wykresu funkcji
| 2 | ||
f(x)= | przez symetrię względem OY | |
| x |
| 2 | −2 | |||
g(x)= | ⇔g(x)= | |||
| −x | x |
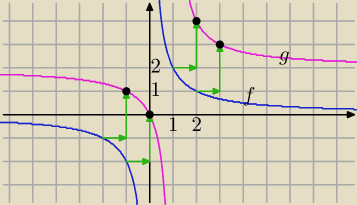 Wzór po przekształceniu wykresu funkcji
Wzór po przekształceniu wykresu funkcji
| 2 | ||
f(x)= | przez translację o wektor [1,2] (przesunięcie równoległe− 1 j. w prawo ,2 j. w | |
| x |
| 2 | ||
g(x)= | +2 | |
| x−1 |
 Bede mial nad czym myslec (chociaz nie jest to straszane )
Tylko on tak troche gmatwa te zgadnienia
Bede mial nad czym myslec (chociaz nie jest to straszane )
Tylko on tak troche gmatwa te zgadnienia