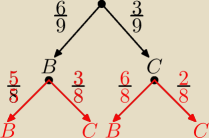
prawdopodobieństwo całkowite, matura Balladyna: "Z urny, w której znajduje się 6 kul białych i 3 czarne losujemy dwie kule. Z pozostałych kul losujemy jedną. Oblicz prawdopodobieństwo tego, że wylosowana kula będzie biała." Przerysowałam tutaj początek mojego drzewka. Jako A oznaczyłam zdarzenie polegające na wylosowaniu za drugim razem kuli białej. Zdarzenie B_i oznacza, że za pierwszym razem wylosowano i∊{0,1,2} kul białych. P(B₀)=³₃₆ co jest dla mnie jasne.to Natomiast nie rozumiem dlaczego P(B₁)=¹⁸₃₆. Nie jestem dobra w rozwiązywaniu tych zadań, nie posługuję się sprawnie schematem drzewka. uprzejmie proszę o wytłumaczenie tego zadania w sposób zrozumiały dla (za przeproszeniem) debila. Bo się pochlastam.

Pytający: W drzewku uwzględniasz kolejność losowania tych dwóch pierwszych kul. Jedną kulę białą wylosowujesz w przypadkach BC i CB. Prawdopodobieństwo zdarzenia B₁ to właśnie prawdopodobieństwo wystąpienia któregoś z tych przypadków.

	6		3		3		6		18
P(B1)=P("BC" lub "CB")=		*		+		*		=		.
	9		8		9		8		36

Balladyna: Kurczę, wszystko wydaje się trudne zanim stanie się proste . Dziękuję.

iteRacj@: Jako zawsze pełna wątpliwości, muszę spytać, czy do rozwiązania tego zadania trzeba narysować w drzewku jeszcze jeden poziom? Bo pytanie dotyczy prawdopodobieństwa tego, że kula wylosowana jako trzecia będzie biała?

Balladyna: Gdy szukałam rozwiązań tego zadania to w drzewku był jeszcze jeden poziom. Tutaj ten trzeci poziom mi się po prostu nie zmieścił

iteRacj@: OK

Pytający: Iteracj@, nie trzeba rysować kolejnego poziomu, bo... w ogóle nie trzeba rysować drzewka.

iteRacj@: najważniejsze to się nie poddawać i liczyć dalej... bez drzewka, z prawdopodobieństwa całkowitego P(T) prawdopodobieństwa tego, że kula wylosowana jako trzecia będzie biała P(B₀) prawdopodobieństwa wylosowania dwóch początkowych kul czarnych P(B₁) prawdopodobieństwa wylosowania wśród początkowych kul jednej białej P(B₂) prawdopodobieństwa wylosowania dwóch początkowych kul białych

	3 2		1
P(B0)=		=
	9 2		12

	6 1   3 1   *		1
P(B1)=		=
	9 2		2

	6 2		5
P(B2)=		=
	9 2		12

P(T) = P(T|B₀)*P(B₀) + P(T|B₁)*P(B₁) +P(T|B₂)*P(B₂)

	6		1		5		1		4		5
P(T) =		*		+		*		+		*
	7		12		7		2		7		12

Balladyna: Metoda bez drzewka bardziej mi odpowiada, wydaje mi się, że już ogarniam to zadanie^^ Wychodzi na to, że w arkuszach z Aksjomatu są błędy w odpowiedziach, to już nie pierwsza taka sytuacja. Dziękuje bardzo!

ite: wieczorem sprawdzę obliczenia, bo jeśli ktoś się myli, to prędzej ja niż Aksjomat....

iteRacj@: czy mój sposób liczenia z 21:46 jest poprawny? można prosić o sprawdzenie?

Pytający: Jak dla mnie prędzej pomylił się Aksjomat niż Iteracj@.

iteRacj@: nareszcie bez błędu , dziękuję za sprawdzenie