Wykres f(|x|-1) ---: Cześć, jak w ogólnym przypadku potraktować funkcję f(|x|−1)? Gdy na liście zadań trafiłem na funkcję f(x)= (¹₂)^|x|−1−1, to wynik na Wolframie mnie trochę zdziwił. Myślałem, że trzeba zrobić najpierw f(|x|), potem przesunąć na prawo (i oczywiście potem w dół)... Wiadomo, że nie jestem tu po wykucie jednego zadania, więc mam pytanie, jak to w ogólnym przypadku rozgryźć?

PW: Narysować wykres f(x) dla x≥0 i jego obraz w symetrii o osi OY (f jest parzysta).

kochanus_niepospolitus: jak już to: f(x) f(|x|) <−−− odbijamy symetrycznie wszystko na prawo od osi OX na ujemną stronę (czyli dla x<0) f(|x| − 1) obniżamy cały wykres o '1'

kochanus_niepospolitus: f(|x| −1) to obniżenie o 1 ale tylko w przypadku gdy f(x) była funkcją liniową

Mila:

	1
f(x)=(		)|x|−1 −1
	2

	1
1) g(x)=(		)x
	2

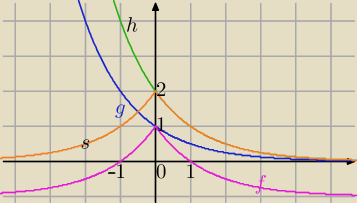
2) przesunięcie wykresu funkcji g(x) o wektor [1,0] ⇒otrzymujesz wykres funkcji:

	1
h(x)=(		)x −1
	2

3) symetria względem OY wykresu z prawej strony OY⇒otrzymujesz wykres funkcji:

	1
s(x)=(		)|x| −1
	2

4) przesunięcie wykresu f. s(x) o wektor [0,−1]⇒otrzymujesz wykres funkcji:

	1
f(x)=(		)|x|−1−1
	2

sprawdzam wartości dla kilku punktów

	1
f(0)=(		)−1 −1=2−1=1
	2

	1
f(−1)=(		1−1 −1=0=f(1)
	2