Geometria analityczna kittylove: przez punkt K o odciętej x=1 poprowadzono dwie styczne do wykresu funkcji f(x)=2x2 −4x −6. Oblicz pole i obwód trójkąta ABK wiedząc, że styczne są prostopadłe, a punkty A i B są punktami styczności.". Błagam, ślężę nad tym już cały weekend

kittylove: Jak wyznaczyć k?

ite: punkt K ma współrzędne K=(1,k) styczne y₁ i y₂ przechodzą przez punkty A=(x_A, y_A)=(x_A, 2x_A²−4x_A−6) B=(x_B, y_B)=(x_B, 2x_B²−4x_B−6) współczynniki kierunkowe stycznych a₁=f'(x_A)=4x_A−4 a₂=f'(x_B)=4x_B−4 f'(x_A)*f'(x_B)=−1 gdyż są prostopadłe (4x_A−4)*( 4x_B−4)=−1 styczne y₁ i y₂ przechodzą przez punkt K y₁= a₁x+b k=a₁*1+b → b=k−a₁ więc y₁= a₁x+k−a₁ y₂= a₂x+b k=a₂*1+b → b=k−a₂ więc y₂= a₂x+k−a₂ y₁= a₁x+b k=a₁*1+b → b=k−a₁ więc y₁= (4x_A−4)x+k−(4x_A−4) y₂= a₂x+b k=a₂*1+b → b=k−a₂ więc y₂= (4x_B−4)x+k−(4x_B−4) styczne y₁ i y₂ mają również równania y₁=f'(x_A)(x−x_A)+y_A=(4x_A−4)*(x−x_A)+2x_A²−4x_A−6 y₂=f'(x_B)(x−x_B)+y_B=(4x_B−4)*(x−x_B)+2x_B²−4x_B−6 z równań stycznych i zależności (4x_A−4)*( 4x_B−4)=−1 tworzymy układ trzech równań z trzema niewiadomymi może ktoś znajdzie krótszy sposób...

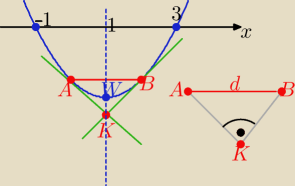
Eta: W(1, −8) to K ∊ do osi symetrii paraboli zatem trójkąt ABK jest prostokątny i równoramienny ( bo A i B są symetryczne względem x=1

	d2
zatem P(ABK)=		, d2=|AB|2 = (xA−xB)2
	2

	xA+xB
xK=1 to		=1 ⇒ xA+xB=2
	2

f^'(x)=4x−4 ⇒ a_AK= 4(x_A−1) i a_BK= 4(x_B−1) z warunku prostopadłości stycznych : (x_A−1)(x_B−1)= −1/16 i x_A+x_B=2 po rozwiązaniu tego układu równań otrzymujemy :

	3		5
xA=		i xB=		zatem |AB|2=d2= 1/4
	4		4

P(ABK) = 1/8 [j²] =============

iteRacj@: @Eta już widziałam, czytałam i ucieszyłam się, że można o wiele szybciej

Eta:

Eta: Mała pomyłka Poprawiam

	d2
P(ABK)=		−−− połowa pola kwadratu o przekątnej "d"
	4

	1
zatem P(ABK)=		[j2]
	16