Ciaglosc funkcji Definicja: Zbadaj ciaglosc funkcji f w zbiorze R a nastepnie sporzadz jej wykres(to sobie daruje ) jesli a) f(x)= {3x dla x<0 {2x−x² x≥0 Tutaj pewnie chodzi o to zeby samemu sobie znalezc punkt x₀ wiec x₀=0 Funkcja jest okreslona dla x₀=0 i f(0)=0 lim x→0⁻ 2x−x²=0 lim x→0⁺ 3x=0 Funkcja jest ciagla w calej dziedzinie b) f(x)={−1 dla x≤0 {1 dla x>0 tutaj x₀=0 Funkcja jest okreslona dla x+0=0 i f(0)=−1 lim x→0⁻ −1= −1 lim x→0⁺ 1 = 1 granica w x₀=0 nie istnieje wobec tego funkcja nie jest ciagla f(x)= |x−1| Ta juz nie wiem Bede mial jeszcze kilak innych z wartoscia bezwzgledna Tutaj bym prosil o poratowanie

iteRacj@: a/ zamieniłeś granica lim_x→0⁻ (3x)=0 lim_x→0⁺ (2x−x²)=0 ale tak f. jest ciągła

iteRacj@: c/ zapisz wzór funkcji przedziałami w klamrze

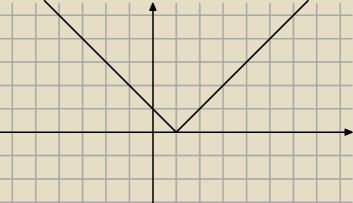
Definicja: Teraz zauwazylem dzieki . w tym f(x)= |x−1| punktem podejrzanym bedzie x₀=1

Definicja: c) f(x)= 1−x dla x<1 x−1 dla x≥1 x₀=1 funkcja jest okreslona dla x₀=1 i f(1)= 0 lim x→1⁻ 1−x= 0 lim x→1⁺ x−1= 0 Funkcja jest ciagla A wydawalo mi sie ze nie bedzie bo jest szpic

iteRacj@: takie ostrza powodują podejrzenie, że nie istnieje pochodna w tym punkcie ciągłości nie szkodzą

Definicja: Taka mam jeszcze funkcje f(x)= |x²−1|

iteRacj@: tak samo wzór funkcji zapisany przedziałami w klamrze

Definicja: czyli tak f(x)= x²−1 dla x∊(−∞,−1> U <1 ,∞) 1−x² dla x∊(−1 , 1) Podejrzanymi puntami nieciaglosci tej funkcji moga byc x₀=−1 i x₀=1 Teraz mam rozpatrywac osobno dla x₀=−1 i x₀=1 ?

iteRacj@: osobno to że funkcja będzie w jednym punkcie ciągła nie oznacza, że jakimś innym będzie też ciągła chyba że jest to funkcja parzysta (ta jest parzysta), ale nie wiem, czy chcesz z tego skorzystać

Definicja: wiec tak dla x₀=−1 i x₀=1 funkcja jest okreslona f(−1)= 0 f(1)=0 Teraz granice lim x→(−1)⁻ 1−x²=0 lim x→(−1)⁺ x²−1= 0 lim x→1⁻ 1−x²= 0 limx →1⁺ x²−1=0 Wniosek . Funkcja jest ciagla .

iteRacj@: zwróc uwagę jaki jest wzór funkcji dla x<−1 jest to x²−1 i dla niej liczysz granicę lewostronną dla argumentu równego −1

Definicja: Inne juz podobnie I na koncu taki przyklad Funkcja sklejana

	|x−4|
f(x)= {		dla x≤−1
	x−4

{ 2x+1 dla −1<x≤1 { 2+2x−x² dla x>1 Tez mam punkty podejrzane o nieciaglosc to x₀=−1 i x₀=1 Teraz pytanie o 1 funkcje

	4−x
Skoro mam dla x≤−1 to musze ja zapisac jako		l nastepne beda juz w takiej
	x−4

postaci jak sa ?

Definicja: Post 21 : 24 jeszcze raz przemysle

iteRacj@: tak, dla x≤−1 f(x)=−1

Definicja: Dziekuje CI bardzo za pomoc Na dzisiaj juz to zakoncze jutro sobie dokoncze